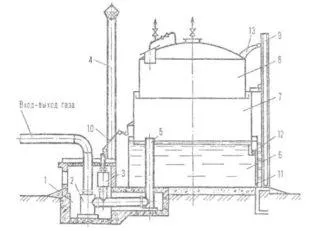
Используя узкий пучок света, расположенный близко к основной оптической оси, можно добиться высокой степени фокусировки. При таком подходе сферическая аберрация становится едва заметной, что детально показано на рисунке 3.
Оптическая сила линзы
Каждому из нас знаком такой предмет, как увеличительное стекло, которое часто используется детективами для тщательного осмотра места преступления, а также бабушками и дедушками для облегчения чтения газет и журналов. Лупа может также агрегировать солнечный свет, причем хулиганы иногда злоупотребляют этим, поджигая траву или деревья, что является опасным занятием и крайне недопустимо! Но тем не менее, полезно изучать свойства света, его путевые лучи и скрытые возможности.
— Обновлено 25 октября 2022 года.
В нашей статье мы подробно рассмотрим следующие темы:
- разберем, что такое линза в физике и какие существуют типы линз;
- обсудим понятие оптической силы линзы, на что она влияет и каковы единицы её измерения;
- ознакомимся с тем, как с помощью математических формул можно рассчитать оптическую силу линзы.
Мы также создадим несколько иллюстраций, поскольку даже самые серьезные физические исследователи любят подкреплять свои объяснения интересными изображениями. 🙂
Что такое линзы
Давайте вспомним ситуации, когда вы сталкивались с такими терминами, как «линза». Они встречаются в очках для коррекции зрения, в объективах фотоаппаратов и в других оптических устройствах. Теперь мы можем более подробно выяснить, что собой представляет линза с точки зрения физики.
Линза — это прозрачное тело, которое может иметь форму либо двух сферических поверхностей, либо комбинации сферической и плоской поверхностей.
Принцип действия линз основан на законах преломления света. Параллельные световые лучи, проходя через линзу, преломляются, тем самым изменяя свое направление; в итоге они могут либо сосредотачиваться в одной точке (фокус), либо рассеиваться в различные стороны.
Виды линз
Линзы классифицируются на две основных группы: собирающие (конвергирующие) и рассеивающие (диффузионные). Названия этих групп сами поясняют их назначение. В свою очередь, как собирающие, так и рассеивающие линзы могут производиться в разных конфигурациях и формах. Давайте подробнее рассмотрим их форму и размеры.
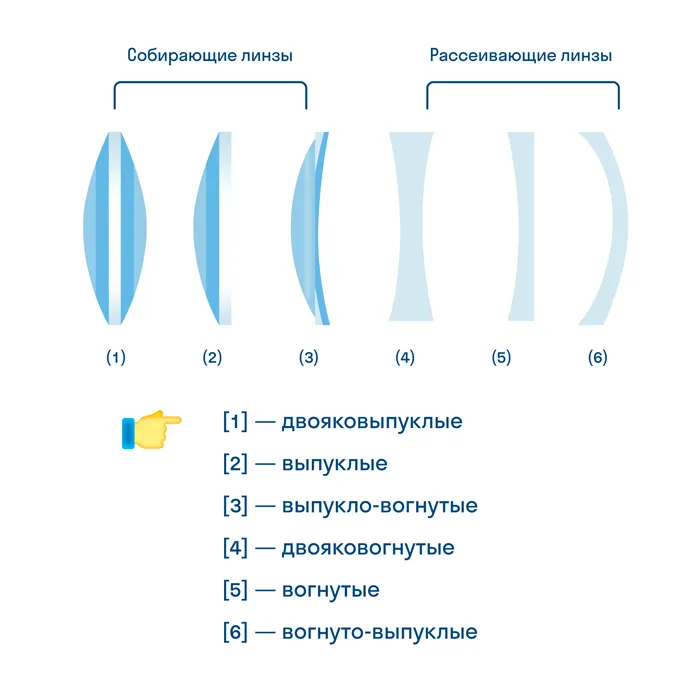
Еще одним важным отличием является то, что у линз, собирающих свет, центр толще краев, тогда как у рассеивающих наоборот — края толще вплоть до центра.
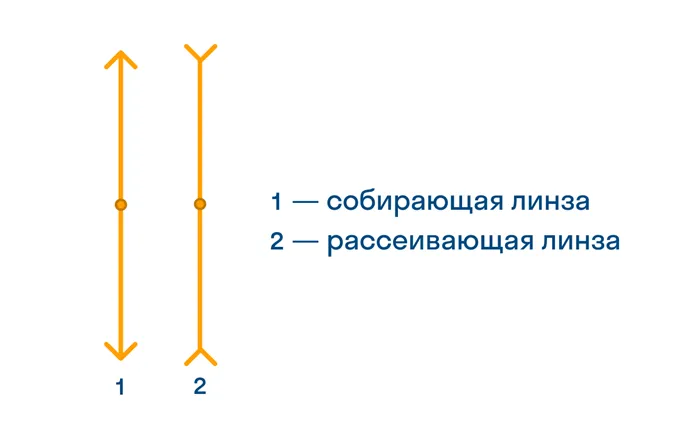
Следует отметить, что при решении физических задач нам не обязательно указывать конкретный тип линзы или выяснять, является ли она полой или выпукло-полой. Для наших расчетов мы будем пользоваться схематическим представлением как собирающей, так и рассеивающей линз.
Как часть образовательной инициативы, Екатерина Мурашова проводит бесплатные занятия для современных родителей. Зарегистрируйтесь для участия в розыгрыше приза, включающего 8 учебных уроков.

Чтобы закрепить полученные знания, мы подводим итоги через формат вопросов и ответов. Вы можете использовать рабочий лист для подготовки к контрольной работе по данной теме: закройте правую ладонь и ответьте на следующие вопросы.
Как называется оптическая сила линзы?
Это способность линзы преломлять лучи света.
Что определяется оптической мощностью?
Оптическая мощность характеризует увеличительную способность линзы.
В каких единицах измеряется оптическая сила линз?
Оптическая сила линз измеряется в диоптриях.
Как можно определить оптическую силу линзы?
Её можно определить по формуле D = 1/F, где
D — оптическая мощность,
F — фокусное расстояние.
Совпадают ли оптические силы собирающей и рассеивающей линзы?
Нет, потому что у рассеивающей линзы продолжения преломленных лучей пересекаются в воображаемой фокальной точке. Оптическая сила рассеивающей линзы обозначается знаком минус, в то время как для собирающей — знаком плюс.
Геометрическая оптика и оптика в общем — это захватывающие области физики. Они не только объясняют поведение световых лучей, но и позволяют создавать удивительные устройства, основанные на этих принципах. Примеры включают в себя телескопы, микроскопы и камеры. Даже в человеческом организме существует оптический прибор — глаз, который дает нам возможность наслаждаться всем прекрасным вокруг нас.
Хотите узнать больше о работе этих световых явлений? Подпишитесь на онлайн-курс физики в Skysmart, чтобы погрузиться в мир науки. Курсы рассказывают о том, как люди с нарушением зрения выбирают очки, возможно ли объяснить физику таких состояний, как астигматизм, близорукость и дальнозоркость и многое другое. Мы с нетерпением ждем вас на курсах — впереди еще много интересного!
Содержание
- 1 История
- 2 Характеристики простых линз
- 3 Ход лучей в тонкой линзе
- 4 Ход лучей в системе линз
- 5 Построение изображения тонкой собирающей линзой
- 6 Формула тонкой линзы
- 7 Линейное увеличение
- 8 Расчет фокусного расстояния и оптической силы линзы
- 9 Комбинация нескольких линз (центрированная система)
- 10 Недостатки простой линзы
- 11 Линзы со специальными свойствами
- 11.1 Линзы из органических полимеров
- 11.2 Линзы из кварца
- 11.3 Линзы из кремния
Первое документальное упоминание о линзах относится к древнегреческой комедии Аристофана «Небулы» (424 год до н.э.), в которой описывается использование изогнутого стекла и солнечного света для создания огня.
Работы Плиния Старшего (23-79 годы н.э.) указывают на то, что подобный способ производства огня был известен и в Римской империи. Проведено также описание возможного использования линз для коррекции зрения; по преданию, Нерон наблюдал за поединками через полый изумруд для коррекции своей близорукости.
Сенека (3 год до н.э. — 65 год н.э.) описал увеличительный эффект стеклянного шара, наполненного водой.
Арабский математик Альхазен (965-1038) написал первую значимую работу по оптике, в которой он объяснял, как хрусталик глаза формирует изображение на сетчатке. Использование линз в очках стало популярным лишь после того, как они появились в Италии около 1280 года.

Мост Золотые Ворота можно видеть через капли дождя, которые действуют как маленькие линзы, преломляющие свет.

Характеристики простых линз
В зависимости от своей формы линзы классифицируются как собирающие (положительные) и рассеивающие (отрицательные). К группе собирающих линз относятся нормальные линзы, как правило, имеющие толщину в центре, которая превышает толщину краев, тогда как у рассеивающих линз имеется обратная ситуация: края их шире по сравнению с центром. Однако эта характеристика применима только в том случае, если коэффициент преломления материала линзы превышает коэффициент преломления окружающей среды. Если же это условие нарушается, ситуация меняется на противоположную. Например, пузырь воздуха, расположенный в воде, может считаться двулучепреломляющей линзой.
Линзы обычно определяются по их оптическим преломляющим свойствам, которые измеряются в диоптриях, либо по фокусному расстоянию.
Для коррекции оптических аберраций (особенно хроматических, возникающих из-за рассеяния света — ахроматичности и обесцвечивания) при создании оптических приборов также важны другие свойства линз и материала, такие как показатель преломления, показатель дисперсии и проницаемость материала в выбранной области оптического диапазона.
Иногда оптические системы (рефракторы) проектируются специально для работы в средах с высокой оптической плотностью (например, иммерсионные микроскопы, использующие иммерсионные жидкости).
Типы линз: собирающие линзы включают 1) двояковыпуклые, 2) плосковыпуклые и 3) вогнуто-выпуклые (положительный (выпуклый) мениск); рассеивающие линзы включают 4) двояковогнутые, 5) плосковогнутые и 6) выпукло-вогнутые (отрицательный (вогнутый) мениск).

Линзы также используются для изменения формы волнового фронта. При прохождении через линзу плоский волновой фронт преобразуется в сферический.


Выпукло-полая линза, называемая мениском, может быть выпуклой (толщина в центре больше) или диффузной (толщина по краям больше), а также телескопической (с фокусным расстоянием на бесконечность). Например, линзы для людей, страдающих близорукостью, часто имеют отрицательный мениск.
Вопреки распространенному заблуждению, оптическая сила мениска с равными радиусами не нулевая, а положительная и зависит от показателя преломления материала и толщины линзы. Мениск, у которого центры кривизны поверхности лежат в одной и той же плоскости, считается концентрической линзой (оптическая преломляющая способность такой линзы всегда отрицательна).
Среди основных свойств сходящейся линзы можно отметить её способность сосредоточивать лучи, падающие на её поверхность, в одну точку, находящуюся по другую сторону от линзы.
Ключевыми элементами линзы являются следующие: NN — оптическая ось — это прямая линия, которая проходит через центры сферических поверхностей, находящихся на границах линзы; O — оптический центр — точка на оптической оси, расположенная внутри линзы (в центре) для выпуклой или биконвексной линзы. Заметьте, что в представлении пути луча предполагается идеализированная (тонкая) линза, без учета преломления на реальной границе раздела. Также показано несколько преувеличенных изображений линзы с двулучепреломлением.
Если перед выпуклой линзой на некотором расстоянии расположено яркое источники света S, осевой световой луч пройдет через линзу без изменения своего направления, в то время как внеосевые лучи будут изгибаться в направлении оптической оси и соединяться в точке F, которая будет изображением S.
Ход лучей в тонкой линзе
Линза, толщина которой можно считать равной нулю, называется «тонкой» в области оптики. Такому объективу не свойственны две главные плоскости, а вместо этого у него имеется одна, где передняя и задняя плоскости полностью сливаются.
Теперь давайте рассмотрим, как строится trajetória света, проходящего через любые точки в тонкой сходящейся линзе. Это достигается благодаря двум свойствам тонкой линзы:
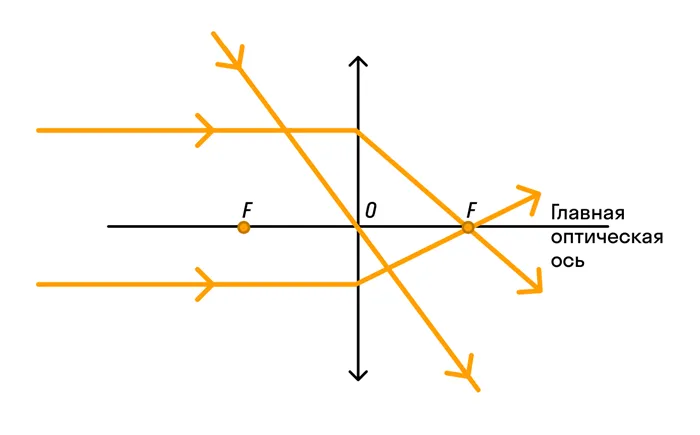
- Луч, проходящий через оптический центр линзы, не изменяет своего направления;
- Параллельные лучи света, проходящие через линзу, сходятся в фокусе.
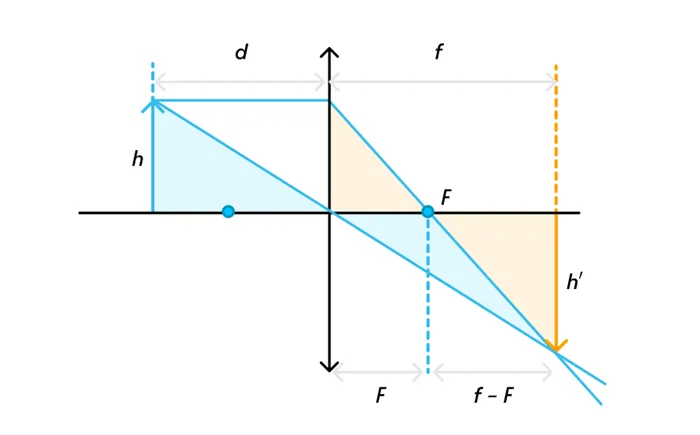
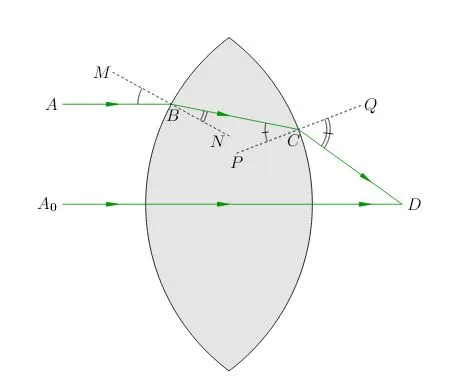
На практике рассмотрим луч SA, который падает на линзу в точке A. Наша задача — построить траекторию после преломления в линзе. Для этого мы также рассмотрим луч OB, который будет параллелен SA и проходить через оптический центр O линзы. Таким образом, согласно первому свойству линзы, OB будет продолжать двигаться, не меняя направления, и будет пересекаться с фокальной плоскостью в точке B. Согласно второму свойству линзы, параллельные лучи SA будут пересекаться в фокусной плоскости после преломления также в одной точке. Таким образом, луч SA пройдет длину AB после прохождения через линзу.
Аналогичным образом можно произвести анализ и для других лучей, например, для SPQ.
Давайте обозначим расстояние от источника света до линзы SO как u, расстояние от точки фокуса до линзы OD как v, а фокусное расстояние как OF — f. Необходимо вывести формулу, которая свяжет эти величины между собой.
Рассмотрим две пары подобных треугольников: один — SOA и остальные — OFB; второй — DOA и DFB. Запишем коэффициенты этих треугольников:
=\frac; \qquad \frac=\frac.» width=»» height=»» />
Поделив первое соотношение на второе, получим следующее:
=\frac; \qquad \frac=\frac — 1.» width=»» height=»» />
После деления обеих частей выражения на v и перестановки членов, мы находим окончательную формулу:
+ \frac = \frac» width=»» height=»» />
где » width=»» height=»» /> — фокусное расстояние тонкой линзы.