Модуль упругой деформации. Модуль юнга в чем измеряется?

С применением данных формул возможно вычислить модуль упругости (мы продемонстрируем это на конкретном примере). Этот закон порождает ряд интересных уравнений, которые могут быть полезны для различных расчетов.

Формула приведенного модуля упругости

Модуль упругости Юнга (также известный как продольный модуль упругости или модуль первого порядка) является ключевым механическим свойством материалов. Он представляет собой меру сопротивления продольным деформациям и отражает уровень жесткости материала. Обозначается буквой E и измеряется в н/м² или па.

Этот параметр играет значительную роль при определении жесткости компонентов, элементов и конструкций, а также при оценке их способности противостоять продольным деформациям. Материалы, используемые в промышленности и строительстве, обычно обладают довольно высокими значениями E. Поэтому на практике значения E выражаются в гигапаскалях (10^9 Па).

Модуль Юнга (E) для стержней можно определить через расчет, в то время как для более сложных материалов его следует измерять при помощи экспериментов.

Приблизительные значения модуля Юнга могут быть получены посредством анализа кривых, полученных в процессе испытаний на растяжение.

Кривая, полученная в испытаниях на растяжение

E представляет собой соотношение между нормальным напряжением σ и относительной деформацией ε.

Закон Гука может быть также представлен с использованием модуля упругости Юнга.

Физический смысл модуля Юнга

Когда материалы подвергаются внешним воздействиям, в них возникает сила, противодействующая этим изменениям, стремящаяся восстановить их исходные форму и размеры упругого тела.

Тем не менее, если материал не сопротивляется деформации и сохраняет свою измененную форму под воздействием нагрузки, такой материал называется абсолютно неупругим или вязким. Хорошим примером такого пластичного материала служит кусок пластилина.

Роберт Гук проводил исследования по удлинению стержней, изготовленных из различных материалов, под воздействием грузов, которые были подвешены к свободному концу. Относительное удлинение, которое вычисляется как отношение абсолютного удлинения к исходной длине, воспринимается как количественное выражение степени изменения формы объекта.

В ходе ряда экспериментов было обнаружено, что абсолютная деформация пропорциональна начальной длине стержня и деформирующей силе F, а также обратно пропорциональна площади поперечного сечения S данного стержня:

Обратная величина α называется модулем Юнга:

e = (Δl) / l = α * (F/S)

Соотношение между растягивающей силой F и площадью поперечного сечения S обозначается как упругие напряжения σ:

Закон Гука, установленный на основании модуля Юнга, можно сформулировать следующим образом:

Теперь мы можем определить физическую сущность модуля упругости: он соответствует напряжению, которое возникает при двойном растяжении образца, выполненного в виде стержня, при условии, что сохраняется непрерывность.

На практике подавляющее большинство испытательных образцов разрушается еще до того, как они достигают половины своей исходной длины. Значение E вычисляется косвенным образом при небольших деформациях.

Коэффициент упругой деформации бруса вдоль его оси можно выразить через формулу k = (ES)/l

Модуль упругости определяет величину динамической энергии упруго деформированных тел или материалов.

Общее понятие

При воздействии внешней силы на объект внутри него возникают контрсилы, которые стремятся компенсировать данное влияние. В идеальных условиях, когда системы находятся в состоянии равновесия, все силы распределены равномерно и уравновешены, что позволяет объекту сохранять свою форму. Однако реальные системы часто не соответствуют этим условиям, что может привести к их деформации. Когда мы рассматриваем прочность материалов, ключевым понятием является упругость.

Определение модуля упругости твердых тел

Упругие материалы — это такие вещества, которые способны вернуться к своей исходной форме после того, как действие внешней силы прекращается.

Внутренние силы равномерно распределены по всей площади поперечного сечения объекта и имеют измеряемую интенсивность, известную как напряжение (p). Оно определяется в ньютонах на квадратный метр (Н/м²) или в системе СИ — паскалях (Па).

Напряжение обладает пространственной ориентацией: нормальное напряжение (σz) направлено перпендикулярно к поверхности поперечного сечения объекта, а касательное напряжение (τz) — в плоскости этого сечения.

Эксперименты с пружинными весами

Модуль упругости (E), представляющий связь между линейной деформацией материала и нормальным напряжением, описывается формулой закона Гука:

где ε — относительная деформация или напряжение.

Переписывая формулу (1) для нахождения нормального напряжения, мы устанавливаем, что E остается постоянным при определенной относительной деформации и называется коэффициентом жесткости. Его единицы измерения включают Па, кгс/мм² или Н/м² :

Модуль упругости служит измерительной единицей зависимости между напряжением, возникающим в материале, и его линейной деформацией, например, во время растяжения или сжатия.

Для эталонного материала модуль упругости указан в мегапаскалях (МПа), поскольку деформации остаются незначительными. Взаимосвязь между этими величинами является обратнопропорциональной. Следовательно, Е имеет высокое значение, которое обычно составляет от 107 до 109.

С помощью данных формул возможно вычислить модуль упругости (это будет продемонстрировано на примере). Этот закон позволяет вывести ряд интересных уравнений, которые могут быть полезны для проведений расчетов.

Модуль упругой деформации

Деформация представляет собой внешний механический эффект на тело, который приводит к изменению его объема и/или формы.

Деформация твердого объекта называется упругой, если она полностью исчезает после того, как нагрузка снимается с этого объекта.

Модуль упругости — это группа параметров, которые характеризуют способность твердого тела к деформациям под воздействием внешнего давления.

В общем смысле модуль упругости (E) можно определить следующим образом.

где — напряжение; — относительная деформация. Стоит отметить, что данное определение актуально для линейной области диаграммы напряжений, то есть в тех случаях, когда деформацию можно считать упругой. В этой части графика значение E определяется наклоном касательной к линейной секции диаграммы.

В зависимости от типа деформации и направления приложенной силы различают различные модули упругости. Наиболее распространенные из них включают:

1. Модуль упругости Юнга,
2. модуль сдвига,
3. модуль упругости массы,
4. коэффициент Пуассона и другие.

Модуль Юнга

Модуль упругости служит для описания деформации при растяжении (сжатии) упругого материала, когда деформирующая сила действует вдоль оси объекта. Обычно модуль упругости рассчитывается на основании закона Гука:

Модуль Юнга представляет собой величину, которая показывает напряжение в брусе, когда его относительная деформация достигает единицы (или удвоенной длины). На практике невозможно достичь удлинения в два раза за счет упругой деформации, за исключением случая резины, когда материал начинает разрушаться.

Связь между модулем упругости и модулем эластичности выражается следующим образом:

где — начальная длина тела; S — площадь поперечного сечения материала.

Единицей измерения модуля упругости является паскаль.

Модуль сдвига

Модуль упругости при сдвиге (G) описывает способность материала сопротивляться изменению формы, при этом объем остается стабильным. Модуль сдвига вычисляется по следующей формуле:

— абсолютное смещение слоев, которые располагаются параллельно друг другу; h — расстояние между слоями; F — сила сдвига, вызывающая перемещение слоев вдоль их направления.

Если вещество является однородным и изотропным, модуль сдвига может быть выражен через модуль упругости следующими формулами.

Этот коэффициент называется коэффициентом Пуассона и зависит от свойств конкретного материала. Кроме того, его иногда обозначают как.

3. Значения расчетных сопротивлений вычисляются путем деления стандартных значений сопротивлений на коэффициенты безопасности материала, округленные до 5 МПа (50 кгс/см²).

Модуль Юнга

Модуль упругости представляет собой физическую величину, которая характеризует способность материала к деформациям под воздействием внешней силы; именно от него зависит жесткость объекта.

Это качество любого материала меняется в зависимости от температуры и давления окружающей среды.

В области физики упругостью называют способность твердых материалов возвращаться к своему исходному состоянию после снятия действующих сил, вызывших деформацию.

Иными словами, когда тело подвергается деформации, возникает сила, стремящаяся вернуть его в исходное состояние и размер. Эта сила называется силой упругости и является результатом электромагнитного взаимодействия между частицами.

Низкие значения модуля упругости свидетельствуют о том, что исследуемое твердое тело обладает высокой упругостью.

Высокие значения модуля упругости указывают на то, что рассматриваемое твердое тело является неупругим или жестким.

Примеры значений модуля упругости:

Таблица

Большинство материалов имеют очень высокие значения модуля упругости, которые обычно обозначаются в «гигапаскалях» (GPa).

Материал	Модуль упругости E, ГПа
Алмаз	1220
Алюминий	69
Дерево	10
Кадмий	50
Латунь	97
Медь	110
Никель	207
Резина	0,9 (≈ 1 МПа)
Сталь	200
Титан	107

Единицы измерения и формулы

В Международной системе единиц (СИ) модуль упругости измеряется в Ньютонах на квадратный метр (Н/м²), что эквивалентно Паскалю (Па).

Формулы

Для вычисления модуля упругости применяют разнообразные формулы, среди которых особенно известен закон Гука.

Закон Гука

Используя предоставленные формулы, можно определить модуль упругости (иллюстрируем на примере). Благодаря этому закону возникают несколько интересных уравнений, которые могут быть полезны для вычислений.

Закон Гука (он объясняет явления в организме с дифференцированным подходом):

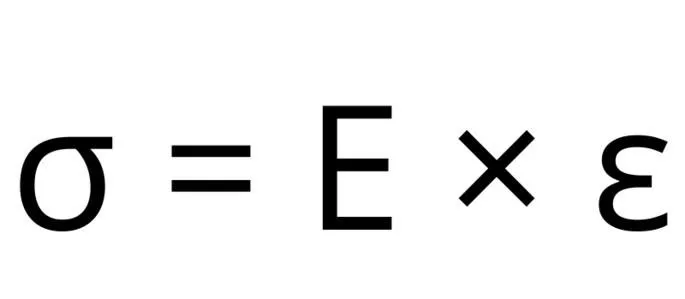
• σ — механическое напряжение
• E — модуль упругости
• e — относительная деформация

Закон Гука (описывает механические свойства материалов)

• Fupr — сила упругости
• k × Δl — удлинение материала
• Fupr — сила упругости
• E — модуль упругости
• S — площадь поперечного сечения
• l — начальная длина материала
• Δl — изменение длины
• Fupr/S — механическое напряжение, обозначаемое как σ
• Δl/l — относительное удлинение, обозначаемое как e

Важно отметить, что данный закон сохраняет свою силу до тех пор, пока материал не претерпит необратимые изменения и не утратит первоначальную форму. Момент, в который это происходит, зависит от конкретного материала. Если рассматриваемый материал обладает высокой жесткостью (что подразумевает большой модуль упругости), то такая точка может совпадать с пределом прочности или значительной деформацией.

Дополнительные формулы для расчета модуля Юнга (модуля упругости)

• E — модуль упругости
• k — жесткость материала
• l — исходная длина стержня
• S — площадь поперечного сечения

Кроме того, жесткость k может быть предложена в следующем виде:

• k — жесткость материала
• E — модуль упругости
• S — площадь поперечного сечения
• l — начальная длина стержня/материала

Пример решения задачи с использованием закона Гука:

Проволока длиной 2,5 м с поперечным сечением 2,5 мм² подвергается растяжению на 1 мм под воздействием силы в 50 Ньютонов. Необходимо вычислить модуль упругости Юнга.

В данном случае мы обратимся к закону Гука (σ = E × e).

Напомним закон Гука:

σ = F / S (где F/S — это механическое напряжение, обозначаемое как σ).

Упругость является свойством твердых тел возвращаться к исходной форме и размерам после снятия внешних деформационных сил.

Модуль упругости различных материалов

Коэффициенты упругости для разных материалов значительно варьируются в зависимости от ряда условий:

• тип веществ, составляющих материал,
• состав материала: однокомпонентный или многокомпонентный (такие как чистые вещества, сплавы и т.д.)
• Структура (металлическая или иная кристаллическая решетка, молекулярная структура и др.)
• Плотность материала (распределение частиц в объеме)
• Обработка, которой он подвергся (запекание, гравировка, прессование и др.).

Справочные данные показывают, что модуль упругости алюминия находится в диапазоне от 61,8 до 73,6 ГПа. Этот показатель может варьироваться в зависимости от состояния металла и метода обработки: для отожженного алюминия он равен 68,5 ГПа.

Значение модуля упругости для медных сплавов зависит не только от их обработки, но и от химического состава:

• Медь — 10,4 ГПа,
• Сплав алюминия с медью для отливок: 10,3 ГПа,
• Медно-фосфорные отливки: 11,3 ГПа.

Модуль упругости латуни также находится на более низком уровне, составляя от 78,5 до 98,1 ГПа, причем высшее значение наблюдается у прокатной латуни.

Чистая медь характеризуется гораздо более высокой устойчивостью к внешним факторам по сравнению с её сплавами — 128,7 ГПа. Однако механическая обработка, включая прокатку, снижает этот показатель:

• Литая медь — 82 ГПа,
• Прокатная медь — 108 ГПа.
• в деформированном состоянии — 112 ГПа,
• холодная вытяжка — 127 ГПа.

Титан (108 ГПа), который признан одним из самых стойких металлов, демонстрирует характеристики, сопоставимые с показателями меди. Свинец, будучи тяжелым и хрупким материалом, показывает значения упругости только в пределах 15,7-16,2 ГПа, что может сравниться по прочности с древесиной.

Для железа взаимосвязь между напряжением и деформацией изменяется в зависимости от метода его обработки: при литье этот показатель варьируется от 100 до 130 ГПа, в то время как при ковке он составляет 196,2-215,8 ГПа.

Чугун, известный своей хрупкостью, демонстрирует соотношение напряжения и деформации в диапазоне 73,6-150 ГПа, что соответствует его классификации. В отличие от него, сталь может иметь модуль упругости, достигающий 235 ГПа.

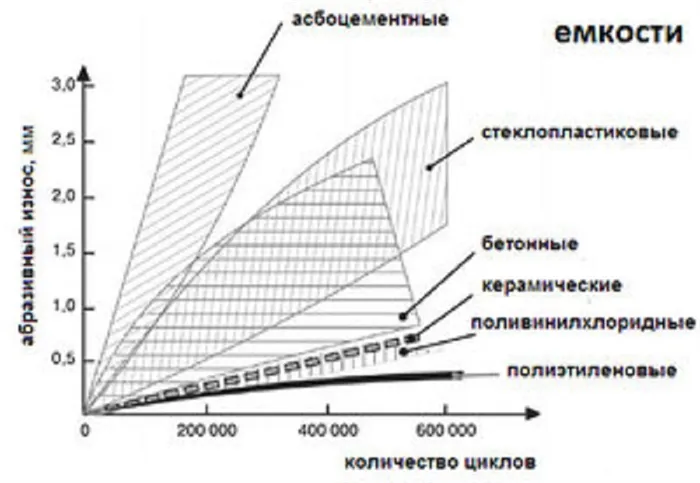
Модуль упругости различных материалов

На параметры прочности также влияет форма изделия. Например, в случае стальных канатов расчеты проводятся с учетом

• диаметра,
• шага пряди,
• угла поворота.

Интересно отметить, что для каната модуль упругости значительно ниже, чем для проволоки с тем же диаметром.

Также следует обратить внимание на прочностные характеристики неметаллических материалов. Например, сосна обладает самым низким значением модуля упругости — 8,8 ГПа, в то время как древесина некоторых лиственных деревьев, известных как «железное дерево», демонстрирует максимальный показатель — 32,5 ГПа. Дуб и бук имеют одинаковое значение, составляющее 16,3 ГПа.

Среди всех строительных материалов прочность гранита на сопротивление внешним нагрузкам составляет всего 35-50 ГПа, что уступает показателю стекла в 78 ГПа. Бетон также меньше по этому критерию, имея значения до 40 ГПа, тогда как известняк и мрамор демонстрируют результаты в 35 и 50 ГПа соответственно.

Гибкие материалы, включая резину и каучук, способны выдерживать осевые нагрузки в пределах от 0,0015 до 0,0079 ГПа.

Модуль упругости — это совокупность характеристик, которые отражают способность твердого тела деформироваться под воздействием нагрузки.

Упругие силы.

При деформации твердого тела его частицы (атомы, молекулы, ионы), находящиеся в узлах кристаллической решетки, покидают свои равновесные позиции. Это перемещение компенсируется силами взаимодействия между частицами, которые удерживают их на определенном расстоянии друг от друга. Таким образом, любой тип упругой деформации создает внутри тела внутренние силы, препятствующие дальнейшей деформации.

Силы, возникающие в теле под воздействием упругой деформации и направленные в сторону смещения частиц, вызванного этой деформацией, именуются упругими силами.

Упругие силы не допускают изменения размеров и формы тела. Они действуют на каждое поперечное сечение деформируемого объекта и на точки контакта с ним. Например, на стороне упруго деформированной плиты D

на расположенную на ней балку C действует сила упругости F π (см. рис. 7).

Ключевой особенностью упругой силы является то, что она всегда перпендикулярна к поверхности контакта между объектами. В ситуации, когда объекты деформированы, например, пружины, сжимаемые или вытягиваемые стержни, веревки или нити, упругая сила ориентирована вдоль их основных осей. Если речь идет о растяжении или сжатии в одном направлении, то сила упругости будет направлена по прямой линии, по которой воздействует внешняя сила, вызывающая изменение формы тела, противодействуя этой силе и оставаясь перпендикулярной к его поверхности.

Сила, которая влияет на объект со стороны опоры или подвеса, называется силой реакции опоры или силой натяжения подвеса.

На иллюстрации 8 представлен ряд примеров силы реакции опоры (силы N1, N2, N3, N4 и N5) и силы натяжения подвеса (силы T1, T2, T3 и T4), которые действуют на объекты.

Значения модуля Юнга для различных материалов

В таблице представлены значения модуля упругости E для некоторых распространенных материалов.

Материал	Модуль упругости E, ГПа
Алюминий	70
Медь	75-125
Вольфрам	350
Графен	1000
Латунь	95
Лед	3
Серебро	80
Серый чугун	110
Сталь	200/210
Стекло	70

Модуль упругости стали в два раза выше, чем у меди и серого чугуна. Этот показатель часто применяется для расчета прочности деталей и изделий в целом.

Какие факторы влияют на модуль упругости бетона В25 и других классов бетонов

На величину модуля упругости оказывают влияние следующие факторы:

• Свойства наполнителя. Их значение находится в прямой зависимости от удельного веса бетона. При низкой плотности модуль упругости оказывается ниже по сравнению с тяжелыми мелкозернистыми строительными материалами, которые используют плотные заполнители из гравия или щебня.
• Классификация бетона. Каждый класс прочности бетона имеет соответствующий модуль упругости. С увеличением класса бетона растет и модуль упругости. Начальное значение модуля упругости для бетона класса В10 равно 19, а для бетона класса В30 – 32,5.
• Эпоха монолита. Параметр, который характеризует модуль упругости материала, напрямую связан со сроком службы. Эта соразмерность не ограничена — чем старше конструкция, тем выше ее прочность. Используя доступные таблицы, производители могут вычислить необходимое значение, применяя соответствующие корректировочные коэффициенты.
• Технологические параметры производства бетона. Технологические процессы, связанные с производством бетона, могут включать как естественное затвердевание при обычных условиях окружающей среды, так и затвердевание в автоклавах под давлением и при высоких температурах. Условия, которые влияют на затвердевание бетона, непосредственно определяют скорость этого процесса.
• Время, необходимое для набора прочности бетоном под нагрузкой. Коэффициент упругости определяется путем умножения значения из таблицы на соответствующий поправочный коэффициент. Для газобетона с ячеистой структурой этот коэффициент составляет 0,7, а для монолитного бетона — 0,85.

Коэффициент упругости различных типов бетона

• Влажность окружающего воздуха. Параметры влажности влияют на содержание влаги в бетоне, что, в свою очередь, отражается на его способности выдерживать конечные нагрузки. Температура среды также оказывает влияние на величину модуля упругости.
• Наличие пространственной сетки из арматурных прутьев. Армирование значительно увеличивает способность бетонной конструкции противостоять разрушительным деформациям и выдерживать активные нагрузки. Проектная прочность арматуры указана в нормативных документах.

Коэффициент упругости напрямую зависит от множества факторов. Эти параметры должны быть учтены при проведении расчетов на прочность. Невзирая на значение модуля упругости материала, стоит отметить, что присутствие арматурных сеток существенно повышает прочность бетона к действующим нагрузкам.

Для повышения прочности рекомендуется использовать арматуру более высокого класса. Обратите внимание, что стандартное значение сопротивления арматуры A6 превышает аналогичное значение арматуры A1.

Параметры Ламе также применяются для описания прочностных характеристик материала. Существует два параметра: m — модуль сдвига и λ. Они позволяют учитывать все изменения в материале в трех измерениях, поэтому зависимость между нормальным напряжением и деформацией представляется следующим образом:

Типы нагрузок

На металлы воздействуют разнообразные статические и динамические нагрузки. В теории прочности обычно выделяют следующие категории нагрузок.

• Сжатие — это процесс, при котором внешняя сила воздействует на объект, вызывая сокращение его длины в направлении приложения нагрузки. Данная форма деформации наблюдается в таких конструкциях, как кровати, опоры, колонны и многих других элементах, предназначенных для поддержки определенного веса. Мосты, эстакады, рамы автомобилей и тракторов, а также фундаменты и арматурные конструкции испытывают постоянное давление.

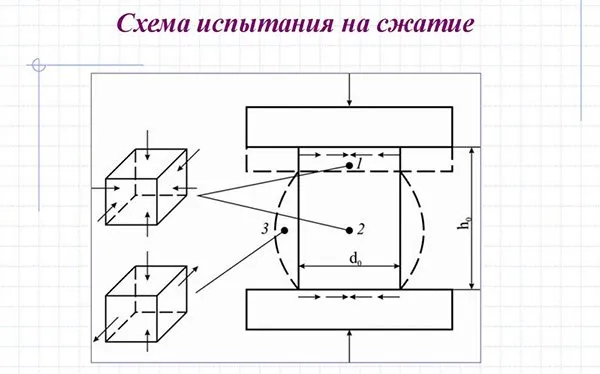
• Деформация представляет собой состояние, при котором нагрузка пытается вытянуть объект в заданном направлении. Аналогичные нагрузки испытывают подъемные и тяговые машины, а также механизмы в процессе подъема и транспортировки различных грузов.

Также читайте: Что такое светодиодные ленты?

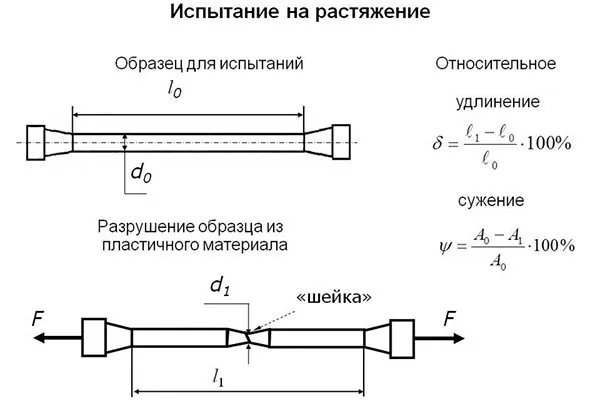
• Сдвиг и срез — данный тип нагрузки возникает, когда силы вдоль одной оси действуют в противоположных направлениях. Крепежные элементы (болты, винты, заклепки и другие материалы) подвержены этому виду нагрузок. При производстве корпусов, металлических рам, зубчатых колес и других деталей механизмов и машин неизбежно используются соединительные компоненты. Их прочность оказывает значительное влияние на эффективность работы оборудования.

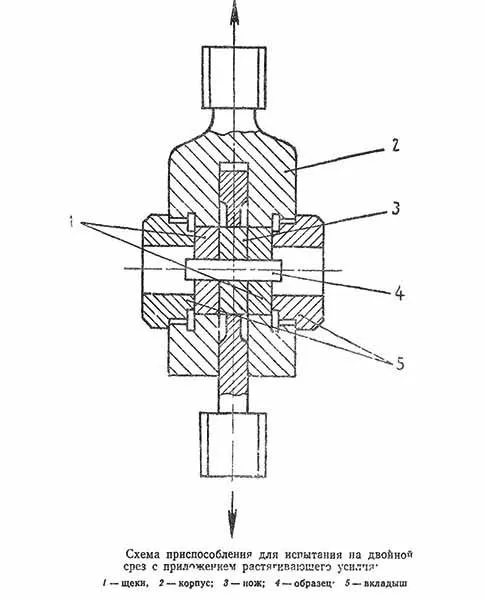
• Кручение — Это явление возникает, когда к объекту прикладывается пара сил, находящихся на определенном расстоянии друг от друга, что приводит к формированию крутящего момента. Эти силы вызывают деформацию объекта в результате кручения. Подобные нагрузки часто встречаются в зубчатых передачах, где валы подвергаются такому типу напряжений. Обычно эти нагрузки не являются постоянными, и величина действующих сил может меняться со временем.

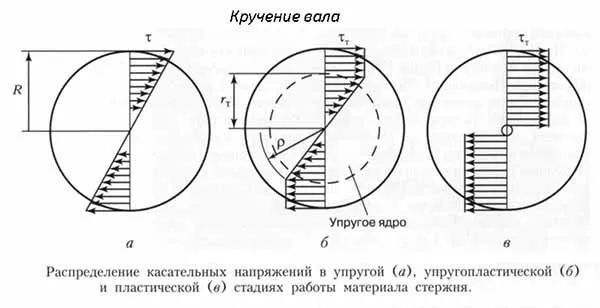
• Изгиб — Это нагрузка, которая влияет на кривизну объекта. Под воздействием таких нагрузок оказываются мосты, поперечные балки, кронштейны, подъемники и другие конструкции.

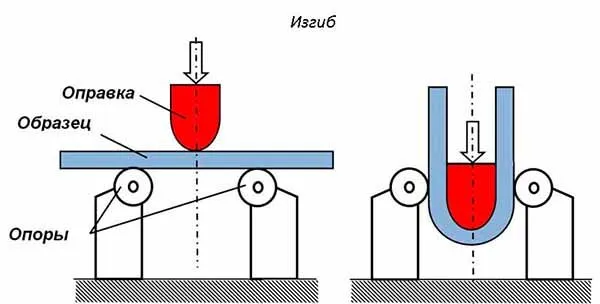
Допустимое механическое напряжение в некоторых материалах при растяжении

Практика показывает, что разные материалы имеют различные уровни сопротивления изменениям своей формы. Прочностные характеристики кристаллических и прочих твердых тел обусловлены силами взаимодействия между атомами. Чем больше расстояние между атомами, тем сильнее силы, удерживающие их вместе. Эти силы достигают своего максимума при некотором уровне напряжения, который приблизительно равен одной десятой от модуля упругости Юнга.

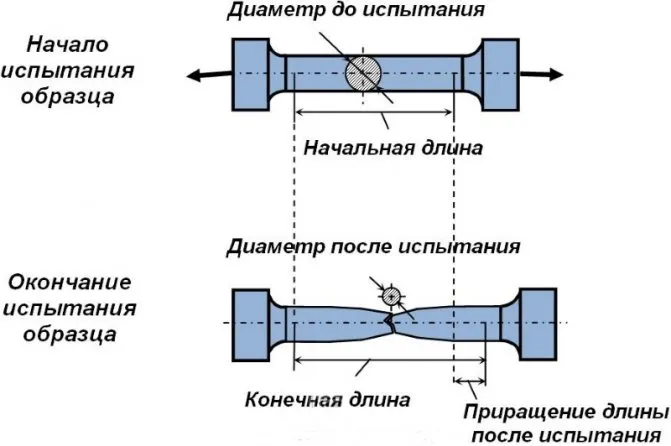
Испытание на растяжение

Это значение именуется теоретической прочностью; когда оно превышается, материал начинает ломаться. На практике разрушение может наступить при значительно более низких значениях, так как реальные образцы материалов имеют неоднородную структуру. Это вызывает неравномерное распределение напряжений, и разрушения начинаются именно в тех областях, где напряжения достигают максимальных значений.

Значения σrast в мегапаскалях (МПа):

Материалы	σrast
Бор (Boron)	5700
Графит	2390
Сапфир	1495
Стальной канат	415
Стекловата	350
Конструкционная сталь	60
Нейлон	48

Эти аспекты принимаются во внимание специалистами при выборе материала для производства будущего изделия. На основании этих факторов также осуществляются расчеты прочности. Например, канаты, предназначенные для подъема и вытягивания, должны иметь запас прочности в десять раз больше их номинальной грузоподъемности. Их необходимо регулярно проверять, подвешивая нагрузку, которая в десять раз превышает эту номинальную грузоподъемность.

Запас прочности, предусмотренный для конструкций, имеющих критическое значение, также варьируется.

Общее понятие

Модуль упругости (также известный как модуль эластичности) представляет собой одно из механических свойств материалов, которое характеризует их прочность на разрыв. Иначе говоря, его значение указывает на пластичность данного материала. Чем выше модуль упругости, тем менее упругим становится брус при равных условиях (нагрузка, площадь поперечного сечения и т.д.).

В области теории упругости модуль Юнга обозначается символом E. Он является ключевым элементом закона Гука, который описывает зависимость между напряжением и деформацией упругих тел.

По стандартам Международной системы единиц, этот параметр измеряется в мегапаскалях (МПа). Однако на практике инженеры предпочитают использовать единицы измерения кгс/см².

Определение модуля упругости осуществляется экспериментальным способом в специализированных научных лабораториях. Этот процесс включает разрушающее испытание образцов материала, выполненных в виде гантелей, на специальном оборудовании. После получения данных о напряжении и деформации при разрушении образца, значения этих величин делятся, что позволяет вычислить модуль упругости Юнга.

Важно отметить, что данный метод подходит для оценки упругости вязких материалов, таких как сталь и медь. В свою очередь, хрупкие материалы, например, чугун и бетон, могут разрушаться при сжатии, приводя к образованию трещин.

Дополнительные характеристики механических свойств

Модуль упругости служит для предсказания поведения материала в условиях сжатия или растяжения. Чтобы учесть другие виды нагрузок, такие как смятие, сдвиг, изгиб и прочие, необходимо использовать дополнительные параметры:

• Жесткость определяется как произведение модуля упругости на площадь поперечного сечения конструкции. Она является мерой пластичности не самого материала, а всей структурной единицы. Измеряется в килограммах силы.
• Относительное удлинение представляет собой отношение абсолютного удлинения образца к его начальной длине. Например, если к бруску длиной 100 мм приложить определённую нагрузку, и он уменьшится на 5 мм, то относительное удлинение будет равно делению этого уменьшения (5 мм) на исходную длину (100 мм), что даст значение 0,05. Эта величина является безразмерной. В некоторых случаях для удобства её могут выразить в процентах.
• Относительная поперечная деформация вычисляется аналогично предыдущему пункту, но вместо длины используется диаметр прутка. Исследования показывают, что для большинства материалов поперечная деформация обычно составляет от 3 до 4 раз меньше продольной деформации.
• Модуль сдвига определяется как отношение относительной продольной деформации к относительной поперечной деформации. Этот параметр играет ключевую роль в описании изменения формы материала под воздействием нагрузки.
• Модуль сдвига описывает упругие характеристики материала в условиях тангенциальной нагрузки, то есть когда сила прикладывается под углом 90 градусов к поверхности образца. К таким нагрузкам можно отнести сдвиговые напряжения в заклепках, гвоздях и других соединениях.
• Объемный модуль упругости показывает, как изменяется объем материала при воздействии равномерной упругой нагрузки. Это соотношение между объемным напряжением и объемной сжимающей деформацией. Примером может служить образец, который помещается в жидкость и подвергается давлению со всех сторон.

Читайте также: Ошибка магнетрона микроволновой печи

Стоит упомянуть, что определенные типы материалов демонстрируют различные механические характеристики в зависимости от направления приложения нагрузки. Такие материалы называются анизотропными. Примерами могут служить дерево, многослойные пластики, некоторые виды камня и текстиль.

Упругие силы препятствуют изменению размеров и формы тел. Эти силы воздействуют на любое поперечное сечение деформируемого объекта и на участки контакта между телами. Например, это справедливо для стороны упруго деформированной плиты D.

Предел прочности материала

Этот предел представляет собой максимальное напряжение, при превышении которого образец начинает разрушаться.

Статическая прочность на растяжение оценивается в условиях, когда деформирующая сила воздействует плавно и непрерывно, в то время как динамическая прочность на растяжение определяется при кратковременном и импульсном воздействии силы. Для большинства материалов предельное значение динамической прочности, как правило, превышает статическое предельное значение.

Устройство для определения прочности на разрыв

Помимо прочности на разрыв, существует также прочность материалов на сжатие и растяжение. Эти характеристики устанавливаются экспериментальным путем на специализированных испытательных стендах, где образцы проходят тестирование с помощью мощных гидравлических машин, оборудованных высокоточными динамометрами и манометрами. В некоторых случаях, когда достичь необходимого давления не представляется возможным hydraulically, для этого используется контролируемый взрыв в герметически запечатанной капсуле.

Допустимые механические напряжения в различных материалах при растяжении

Практика демонстрирует, что разные материалы обладают различной способностью к деформации. Механические характеристики кристаллических и других твердых тел обусловлены межатомными взаимодействиями. Чем больше расстояние между атомами, тем более интенсивные силы притягивают их друг к другу. Эти силы достигают своего пика при определенном уровне напряжения, который составляет примерно одну десятую часть модуля Юнга.

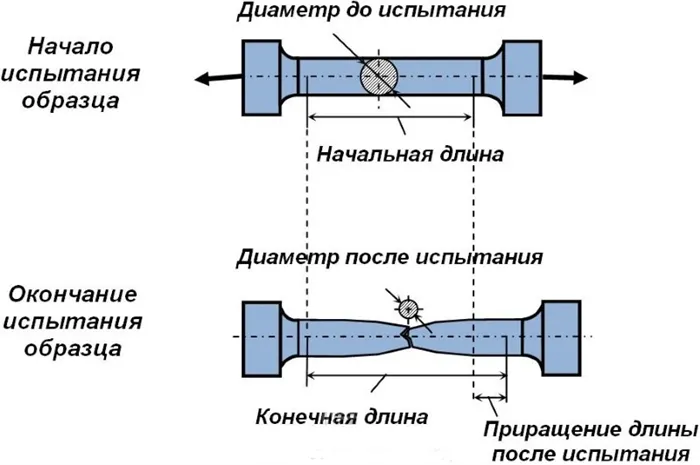
Испытания на растяжение

Это значение известно как теоретическая прочность; когда оно превышается, материал начинает терять свою целостность. На практике разрушение начинается при значениях, которые ниже теоретических, поскольку реальные образцы имеют неоднородную структуру. Это приводит к неравномерному распределению напряжений, и разрушение начинается именно в тех областях, где напряжения достигают своих максимальных значений.

Материалы	σ rast
Материалы из бора	5700	0,083
Графит	2390	0,023
Сапфир	1495	0,030
Стальная проволока	415	0,01
Стекловата	350	0,034
Конструкционная сталь	60	0,003
Нейлон	48	0,0025

При выборе материалов для создания изделий дизайнеры учитывают множество факторов. Эти данные служат основой для расчетов прочности. Например, канаты, предназначенные для подъема и вытягивания, должны иметь запас прочности в десять раз больше их предельной нагрузочной способности. Регулярные проверки их состояния осуществляются путем подвешивания груза, который в десять раз превышает номинальную грузоподъемность каната.

Заранее предусмотренный запас прочности критически важных конструкций также может быть различным.

Коэффициент запаса прочности

Коэффициент безопасности служит для количественной оценки способности изделия выдерживать нагрузки, превышающие его номинальные параметры. Он отражает возможность предмета справляться с перегрузками. Для бытовых товаров такой коэффициент обычно невысок, однако для критически важных компонентов и деталей, повреждение которых может создать угрозу жизни и здоровью человека, он должен быть значительно выше.

Верный расчет прочностных характеристик обеспечивает необходимый запас прочности, не создавая при этом чрезмерной нагрузки на конструкцию и не снижая ее эксплуатационные показатели. Для выполнения этих расчетов применяются сложные математические методы и современные компьютерные программы. Ключевые структуры подвергаются расчетам на суперкомпьютерах.