Чтобы рассчитать модуль упругости и научиться его применять, можно обратить внимание на простой пример с пружиной. Возьмите металлическую пружину и измерьте площадь круга, который создают ее витки. Для этого применяется следующая формула: S = πr², где π — это число пи, приближенно равное 3,14, а r — радиус витков пружины.
Модуль упругости — что это такое? Определение модуля упругости для материалов
Перед тем как использовать материал в строительстве, важно ознакомиться с его физическими характеристиками, чтобы знать, как правильно обращаться с ним, какие механические нагрузки допустимы для данного материала и так далее. Одним из ключевых свойств, имеющих большое значение, является модуль упругости.
В данном разделе мы проанализируем, что такое упругость и каково ее значение относительно одного из наиболее распространенных строительных материалов – стали. Также мы рассмотрим подобные аспекты в отношении других материалов для сравнения.
История изучения упругости материалов
Физическая теория упругих тел и их реакция на внешние нагрузки была тщательно исследована английским ученым Томасом Юнгом в 19 веке. Однако сама идея упругости была сформулирована еще в 1727 году швейцарским математиком, физиком и философом Леонгардом Эйлером. Первые эксперименты по измерению модуля упругости были проведены венецианским математиком и философом Якопо Рикатти в 1782 году, за четверть века до исследований Юнга.
Томас Юнг внес значительный вклад в развитие теории упругости, придавая ей современную форму, которая позже была оформлена в известный закон Гука, как в его базовом, так и в обобщенном варианте.
Физическая природа упругости
Любое тело состоит из атомов, на которые действуют как притягательные, так и отталкивающие силы. Соотношение этих сил определяет состояние и характеристики материи в заданных условиях. При приложении небольшой внешней растягивающей или сжимающей силы атомы твердого тела начинают перемещаться, создавая противодействующую силу равной величины, которая направлена на возвращение атомов в исходное положение.
При перемещении атомов в системе наблюдается увеличение энергии всего комплекса. Исследования показывают, что для небольших деформаций энергия прямо пропорциональна квадрату величины этих деформаций. Это указывает на то, что сила, являясь производной от энергии, пропорциональна первой степени деформации, то есть линейно зависит от неё. Ответ на вопрос о том, что такое модуль упругости: это коэффициент, который связывает силу, приложенную к атому, и деформацию, вызванную этой силой. Размерность модуля Юнга совпадает с размерностью давления, выраженной в паскалях.
Древесина классифицируется как анизотропный материал, так как её волокна располагаются в определённом направлении. Модуль упругости древесины измеряется вдоль направления волокон и значительно ниже (на 1-2 порядка) по сравнению с радиальными и тангенциальными направлениями. Понимание модуля упругости древесины является ключевым фактором при проектировании конструкций из древесных материалов.
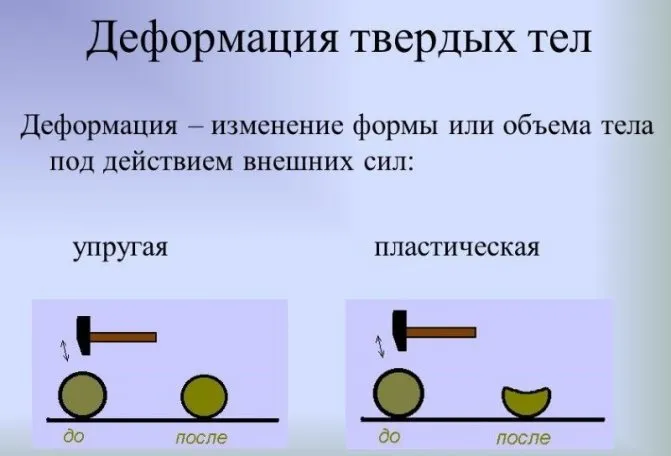
Пластичность и хрупкость
Тело, выполненное из любого материала, будет демонстрировать упругие свойства при небольших деформациях. Однако большинство тел способно на пластические деформации в различной степени. Существуют также хрупкие материалы.
Механические характеристики различных материалов могут значительно различаться. Например, такие материалы, как резина или сталь, показывают упругие свойства при относительно высоких уровнях напряжения и деформации. Для стали закон Гука применим до тех пор, пока не будут достигнуты предельные значения deformations.
Для резины характерны существенно более высокие значения ε, достигающие нескольких десятков процентов. Именно поэтому такие материалы классифицируют как эластичные.
Жидкая глина, пластилин или свинец обладают ограниченным диапазоном упругой деформации. Вещества, для которых небольшие нагрузки вызывают пластическую деформацию, принято называть вязкими материалами.
Классификация материалов на упругие и пластичные является достаточно условной. В зависимости от приложенных напряжений один и тот же материал может вести себя либо упруго, либо пластично. Например, сталь демонстрирует вязкие свойства при значительных напряжениях. Это свойство активно используется в процессе уплотнения стальных изделий при помощи прессов, создающих мощные напряжения.
Ковать холодную сталь или железо с помощью молота довольно сложно. Однако эти материалы можно легко формировать через горячую ковку. Свинец, который при нормальной температуре является податливым, становится более упругим при охлаждении до значения ниже -100°C.
Одним из важных свойств твердых тел является их хрупкость, которая имеет значительное значение в практике.
Тело считается хрупким, если оно подвержено разрушению при незначительных деформациях. Например, стекло и фарфор относятся к хрупким материалам: они могут разбиться при падении на поверхность даже с небольшой высоты. Чугун, мрамор и янтарь также имеют высокую степень хрупкости. Напротив, сталь, медь и свинец не подвергаются такому разрушению. Особенности хрупких материалов лучше всего отражаются в соотношении σ.
Напряжение зависит от деформации. На рисунках 11, a и b представлены диаграммы растяжения для чугуна и стали. Явно видно, что увеличение длины чугуна всего на 0,1% приводит к возникновению напряжения около 80 МПа, в то время как напряжение в стали при аналогичном удлинении составляет лишь 20 МПа.
Рис. 11 Чугун разрушается сразу при удлинении 0,45 %, практически не проходя через стадию предварительной пластической деформации. Его прочность на разрыв достигает 1,2∙10^8 Па. Напротив, сталь может выдерживать растягивающее напряжение до 1,5 бар.
При значении = 0,45 % деформация ещё сохраняет упругие характеристики, и разрушение происходит при ε ≈ 15 %. Предел прочности стали на разрыв равен 700 МПа.
Во всех хрупких материалах напряжение возрастает очень быстро с увеличением деформации, и они разрушаются при относительно низких уровнях напряжения. Хрупкие материалы практически лишены пластических свойств.
Физический смысл модуля Юнга
Когда объект сталкивается с необходимостью изменить свою форму, внутри него возникают силы, которые противодействуют этому изменению и стремятся вернуть материал к его изначальным форме и размерам.
Если же тело не противопоставляет силы при изменении формы и остается в новом деформированном состоянии, то такое тело называют абсолютно неупругим или пластичным. Ярким примером пластичного тела является кусок пластилина.
Р. Гук провел исследования, касающиеся удлинения стержней из различных материалов под воздействием нагрузок, прикрепленных к свободному концу. Относительное удлинение, представляющее собой соотношение абсолютного удлинения к первоначальной длине, является числовым показателем степени изменения формы.
В ходе серии экспериментов было установлено, что абсолютная деформация находится в прямой зависимости от исходной длины прутка и силы деформации F, а также обратно пропорциональна площади его поперечного сечения S:
Обратное значение α называется модулем упругости Юнга:
e = (Δl) / l = α * (F/S)
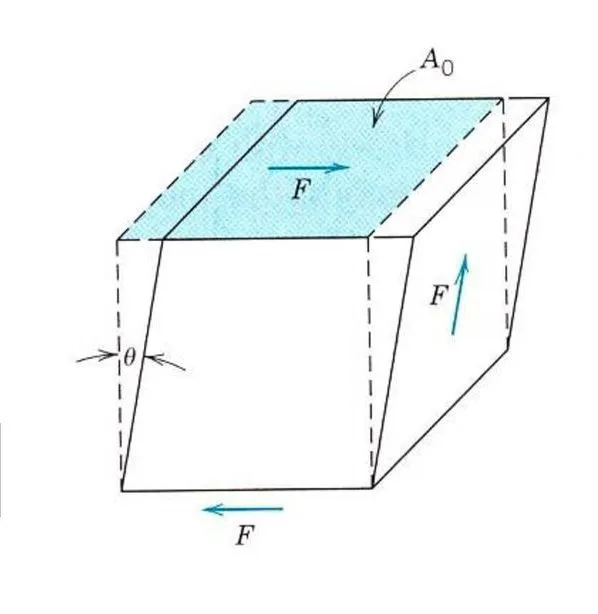
Соотношение между растягивающей силой F и площадью поперечного сечения S обозначается как упругое напряжение σ:
Закон Гука, основанный на модуле упругости Юнга, формируется следующим образом:
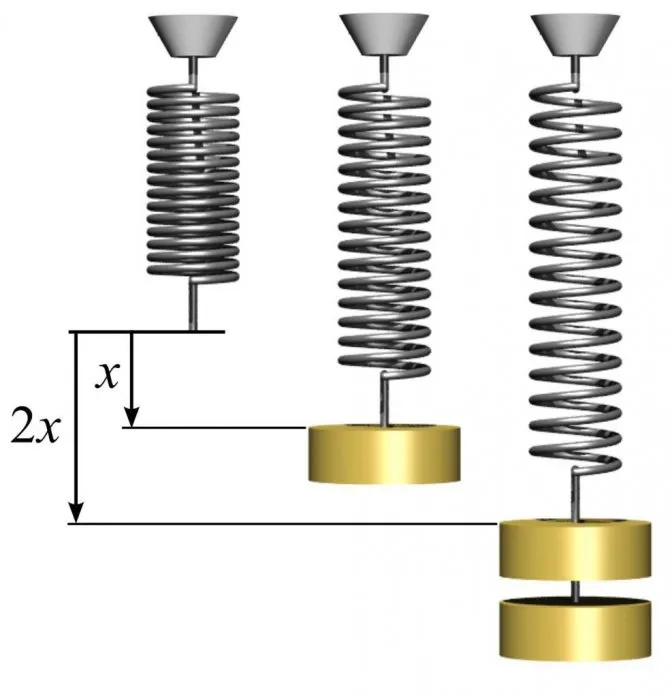
Теперь мы можем выразить физический смысл модуля упругости: он характеризует напряжение, которое возникает при удвоенном растяжении образца, выполненного в виде стержня, при сохранении его непрерывности.
На практике, подавляющее большинство материалов разрушается до момента, когда они достигают удвоенной своей начальной длины. Значение модуля упругости E вычисляется косвенным образом при низких уровнях напряжения.
Коэффициент жесткости для упругой деформации бруса вдоль его оси определяется по формуле k = (ES) / l.
Модуль упругости определяет количество динамической энергии тел или материалов, которые подверглись упругой деформации.
Силы упругости.
В процессе деформации твердого тела его компоненты (атомы, молекулы, ионы), находящиеся в узлах кристаллической решетки, смещаются из своего равновесного положения. Это движение сдерживается силами взаимодействия между частицами твердого вещества, которые удерживают их на заданном расстоянии друг от друга. Таким образом, любой вид упругой деформации создает внутри тела силы, которые препятствуют его дополнительной деформации.
Силы, возникающие в теле в ответ на его упругую деформацию и направленные в сторону смещения частиц, вызванного данной деформацией, называются упругими силами.
Упругие силы не позволяют телу изменять свои размеры и форму. Эти силы действуют на любом сечении деформируемого объекта, а также в точке соприкосновения с ним. Например, на плите D, которая подверглась упругой деформации, на балку C, расположенную на ней, воздействует сила упругости F π (см. рисунок 7).
Одной из ключевых характеристик упругой силы является ее перпендикулярная направленность к поверхности контакта между взаимодействующими телами. В контексте деформируемых объектов, таких как пружины, сжатые или растянутые стержни, шнуры и нити, упругая сила проявляет себя вдоль их осей. При одностороннем растяжении или сжатии сила упругости должна быть направлена по прямой линии, которая соответствует внешней силе, вызывающей деформацию объекта. Эта сила обратно пропорциональна направлению приложенной силы и перпендикулярна самой поверхности тела.
Сила, оказываемая на тело со стороны опоры или подвеса, называется реакционной силой опоры или силой натяжения подвеса.
На рисунке 8 представлены примеры реакционных сил опоры (силы N1, N2, N3, N4 и N5) и сил натяжения подвеса (силы T1, T2, T3 и T4), действующих на объекты.
Модуль Юнга (или модуль упругости первого рода) представляет собой ключевую механическую характеристику материи. Он служит показателем сопротивления продольной деформации и отражает уровень жесткости материала. Обозначается буквой E и измеряется в н/м² (паундах на квадратный метр).
Физическая основа упругости
Каждое физическое тело состоит из атомов, между которыми действуют как притягивающие, так и отталкивающие силы. Равновесие этих сил определяет состояние и свойства материала при определённых условиях. Когда к твердым телам применяется небольшая внешняя растягивающая или сжимающая сила, атомы начинают смещаться, создавая противодействующую силу, равную по величине и направленную обратно, стремящуюся вернуть атомы в их первоначальное состояние.
При перемещении атомов происходит увеличение энергии всей системы. Исследования показывают, что для небольших деформаций энергия пропорциональна квадрату величины этих деформаций. Это указывает на то, что сила, являющаяся производной от энергии, пропорциональна первой степени величины деформации, то есть она линейно зависит от этой величины. Ответ на вопрос о том, что такое модуль упругости, звучит следующим образом: это коэффициент пропорциональности между силой, действующей на атом, и деформацией, вызванной этой силой. Размерность модуля упругости Юнга совпадает с размерностью давления (Па).
Нормативные данные для расчетов железобетонных конструкций:
(вернуться к списку таблиц)
Таблица 2. Начальные модули упругости бетона (в соответствии с СП 52-101-2003)
(вернуться к списку таблиц)
Таблица 2.1. Начальные модули упругости бетона согласно СНиП 2.03.01-84*(1996)
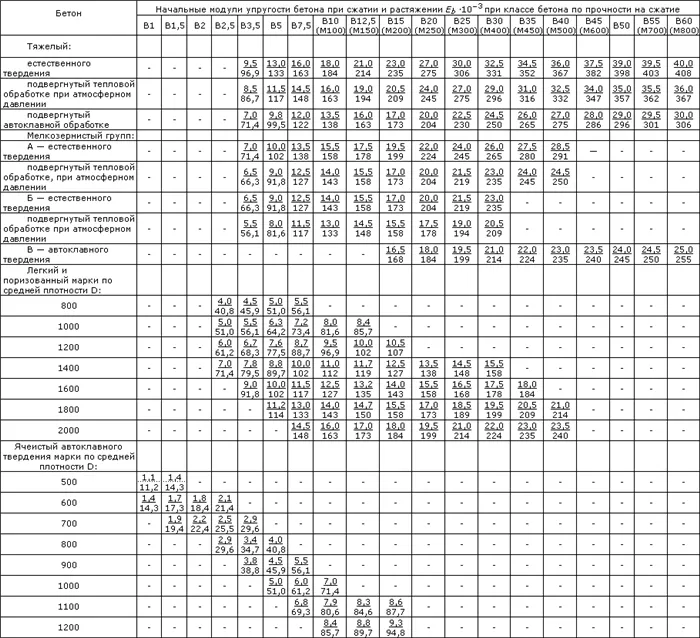
Примечания: 1. Над чертой значения представлены в МПа, под чертой — в кгс/см².
2. Для легких, ячеистых и газобетонов со средней плотностью бетона начальный модуль упругости вычисляется с использованием линейной интерполяции.
3. Для неавтоклавного газобетона значения Eb аналогичны таковым для автоклавного бетона, умноженные на коэффициент 0,8.
4. Для напряженного бетона значения Eb принимаются такими же, как у тяжелого бетона, умноженные на коэффициент a = 0,56 + 0,006B.
5. Марки бетона, указанные в скобках, могут не точно соответствовать перечисленным маркам бетона.
Таблица 3. Нормативные значения прочности бетона (в соответствии с СП 52-101-2003)
(вернуться к списку таблиц)
Таблица 4. Расчетные значения прочности бетона (в соответствии с СП 52-101-2003)
(вернуться к списку таблиц)
Таблица 4.1. Расчетные значения сопротивления бетона сжатию согласно СНиП 2.03.01-84*(1996)
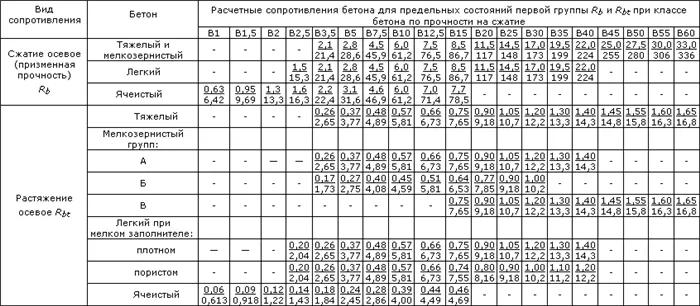
Таблица 5. Расчетные значения сопротивления бетона растяжению (согласно СП 52-101-2003)
(вернуться к списку таблиц)
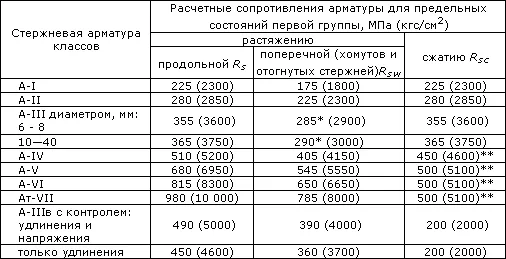
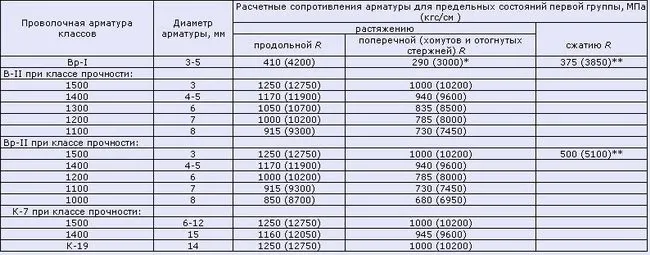
Таблица 6. Нормативные сопротивления для арматуры (согласно СП 52-101-2003)
(вернуться к списку таблиц)
Также рекомендую ознакомиться с: Свойства и использование электродов для сварки переменным током
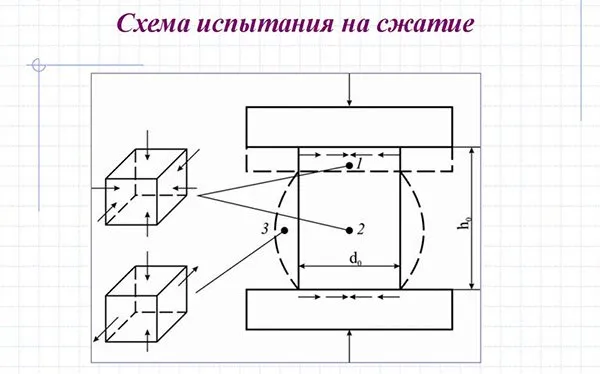
Таблица 6.1 Нормативные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)

Таблица 6.2. Нормативные сопротивления для арматуры классов В и К согласно СНиП 2.03.01-84* (1996)
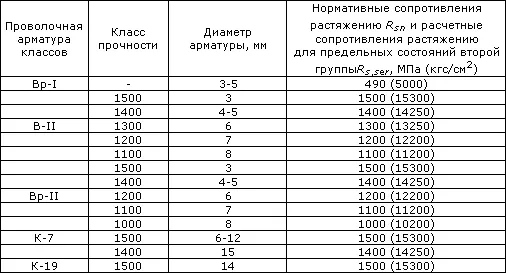
Таблица 7. Расчетные сопротивления для арматуры(согласно СП 52-101-2003)
(назад к перечню таблиц)

Таблица 7.1. Расчетные сопротивления для арматуры класса А согласно СНиП 2.03.01-84* (1996)
Предел упругости материалов
Модуль упругости представляет собой величину напряжения, необходимую для деформации твердого тела на 100%. Тем не менее, все твердые материалы обладают модулем упругости, который составляет лишь 1% от их общей деформации. Это означает, что если объект подвергается воздействию силы, и его деформация остается ниже 1%, то после освобождения от этой силы он полностью восстановит свою первозданную форму и размеры. Однако, если сила оказывается чрезмерной и деформация превышает 1%, тело не сможет вернуться к своим исходным размерам после прекращения воздействия внешней силы. В таких случаях говорят о постоянной деформации, которая указывает на то, что предел упругости материала был превышен.
Когда брус испытывает нагрузку, помимо продольной деформации ε, возникает также поперечная деформация ε1. Поперечное напряжение или коэффициент Пуассона m представляют собой отношение ε1 к ε.
Коэффициент Пуассона для древесины определяется на основе испытаний прямоугольных призматических образцов с размерами 40 x 40 мм и высотой 150 мм. Для этого процесса к образцам прикрепляют шесть тензометров с базой 20 мм и коэффициентом передачи, равным примерно 1000. Из этих тензометров два предназначены для регистрации продольной деформации (деформация в направлении приложенной силы сжатия), в то время как остальные четыре измеряют поперечную деформацию в двух направлениях, взаимно перпендикулярных друг другу. Каждый из образцов проходит испытание при шести загрузках: 400 и 1600 кг для сжатия вдоль волокон, а также 40 и 160 кг для сжатия поперек волокон.
Для древесины сосны и ели коэффициент Пуассона при сжатии вдоль волокон составляет v0 = 0,5.
При нагреве цветных металлов и их сплавов их прочностные характеристики сразу же снижаются, а при температурах около 600 °C практически теряются. Исключение составляет алюминий-хром, прочность на разрыв которого возрастает с увеличением температуры и достигает максимального значения при 1100 °C, где σin1100 = 2σin20.
Модуль упругости стали
В процессе проектирования изделий или компонентов из стали важно учитывать сплавы с точки зрения их устойчивости к различным видам механических напряжений: ударам, изгибам, растяжению и сжатию. Параметр модуля упругости стали, вместе с её твердостью и другими значениями, предоставляет информацию о высокой стойкости материала к указанным воздействиям.
В железобетонных конструкциях применяются как продольные, так и поперечные арматурные стержни. В горизонтальной плоскости они испытывают растягивающее напряжение, а в вертикальной — действуют под тяжестью всей конструкции. В зонах с высокой концентрацией напряжений, таких как углы, технические проемы, лифтовые шахты и лестничные марши, используется увеличенное количество арматуры. Пористая структура бетона, способная поглощать воду, приводит к постоянным колебаниям сжимающего и растягивающего напряжения.
Рассмотрим другой пример. В период военных конфликтов в авиационной сфере происходило множество значительных событий. Одними из самых частых причин аварий являлись возгорания двигателей. Когда самолет взлетает, он оказывается в условиях разреженного воздуха, что приводит к расширению фюзеляжа, а при посадке этот процесс происходит наоборот. Кроме того, на конструкцию самолета воздействуют факторы такие, как сопротивление воздушных потоков, давление искривленных слоев воздуха и множество других сил. Несмотря на высокую прочность, доступные в то время металлические сплавы не всегда соответствовали требованиям для критически важных компонентов, что, в частности, способствовало разрушению топливных баков.
В разных отраслях промышленности сталь применяется для создания подвижных элементов, таких как пружины и рессоры. Сортам стали, предназначенным для этих целей, свойственна высокая стойкость к растрескиванию при изменяющихся нагрузках.
Модуль упругости стали
Упругость твердых тел обозначает их возможность возвращаться к первоначальной форме после устранения воздействия деформирующих сил. Например, стержень, сделанный из пластилина, не проявляет упругости, в то время как резина может быть сжата и растянута. При воздействии различных сил на предметы и материалы они подвергаются деформации. В зависимости от физических характеристик твердых тел выделяются два типа деформации:
- Эластичная — эффект исчезает после прекращения действия внешних сил,
- Пластическая — необратимое изменение формы.
Модуль упругости представляет собой совокупность различных физических величин, которые характеризуют склонность твердого тела к упругой деформации.
Данная концепция была впервые сформулирована Томасом Юнгом. Исследователь подвешивал грузы на металлические стержни и фиксировал их удлинение. Некоторые образцы увеличивались в длине в два раза, а другие разрушались в ходе эксперимента.
Сегодня это определение охватывает ряд физических характеристик тел:
Модуль упругости: вычисляется по формуле E= σ/ε, где σ — напряжение, которое соответствует силе, деленной на площадь ее приложения, а ε — упругая деформация, характеризующаяся соотношением между изначальной деформацией образца и его сжатием после завершения этого процесса.
Модуль сдвига (G или m) представляет собой способность материала сопротивляться деформациям при приложении касательных нагрузок, сохраняя при этом свой объем. К примеру, если верхняя часть гвоздя не имеет формы прямого угла, то при его забивании материал может изменять свою форму. Это значение применяется в расчетах прочности для анализа сдвига и кручения.
Объемный модуль упругости, также известный как коэффициент объемного сжатия (K), описывает изменения, возникающие под воздействием всестороннего напряжения, например, при действии гидростатического давления.
Коэффициент Пуассона (ν или m) оценивает соотношение между поперечным сжатием и продольной деформацией, рассчитанное по образцам определенного материала. Для абсолютно хрупких материалов этот коэффициент равен нулю.
Константа Ламе — это энергия, способствующая возвращению материала к его изначальной форме, и она рассчитывается с помощью формирования скалярных комбинаций.
Модуль упругости стали тесно связан с рядом других физических характеристик. Например, во время испытаний на растяжение необходимо учитывать предел прочности, при достижении которого происходит разрушение материала.
- Связь между жесткостью и пластичностью,
- ударная стойкость,
- мощность разряда,
- прочность на растяжение и сжатие (как поперечное, так и продольное),
- устойчивость к удачным, динамическим и другим видам нагрузок.
Разнообразие методов эксплуатации материалов обусловлено необходимостью соответствия механическим характеристикам, установленным в разных секторах промышленности, а также при создании конструкций и устройств.
Твердые вещества обладают определенной несущей способностью, превышение которой может привести к разрушению металлической матрицы, появлению заметных осколков или микротрещин. Появление дефектов связано с ухудшением эксплуатационных свойств или полным выходом из строя. Прочностные характеристики сплавов и готовой продукции подвергаются испытаниям на специализированных стендах. В стандартах предусмотрены следующие виды испытаний:
- Постоянное воздействие силы деформации,
- Краткосрочные и долговременные воздействия,
- Нагрузки на растяжение и сжатие,
- Гидравлические давления и т.д.
В сложных механизмах и системах, отказ одного элемента часто приводит к повышению нагрузки на остальные. Как правило, сбои начинаются именно в тех местах, где нагрузка наиболее интенсивная. Запас прочности играет ключевую роль в обеспечении безопасности во время аварийных ситуаций и в продлении срока эксплуатации оборудования.
Одним из самых распространенных цветных металлов, применяемых в промышленности, является медь, известная под латинским названием cuprum. Это название происходит от имени острова Кипр, где греки добывали медь много тысяч лет назад. Медь относится к числу семи металлов, известных с древних времён, и используется для производства ювелирных украшений, сосудов, монет и инструментов.
Допустимое механическое напряжение в некоторых материалах при растяжении
Из опыта жизни известно, что различные материалы по-разному реагируют на изменения формы. Прочностные характеристики кристаллических и других твердых веществ определяются межатомными взаимодействиями. Чем больше расстояние между атомами, тем сильнее силы, которые притягивают их друг к другу. Эти силы достигают своего пика при определённом уровне напряжения, который составляет примерно одну десятую от модуля упругости Юнга.
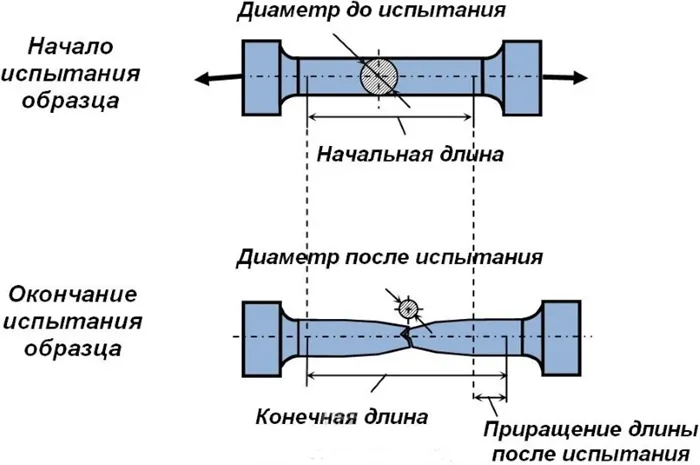
Испытание на растяжение
Это значение известно как теоретическая прочность; как только оно превышается, материал начинает разрушаться. На практике разрушение происходит при более низких уровнях нагрузки, поскольку реальные образцы обладают неоднородной структурой. Это приводит к неравномерному распределению напряжений, и разрушение возникает в тех участках, где напряжения максимальны.
Значения σrast в МПа:
| Материалы | Материалы σrast | |
| Материалы srast Boron | 5700 | 0,083 |
| Графит | 2390 | 0,023 |
| Сапфир | 1495 | 0,030 |
| Стальная проволока | 415 | 0,01 |
| Стекловата | 350 | 0,034 |
| Конструкционная сталь | 60 | 0,003 |
| Нейлон | 48 | 0,0025 |
Дизайнеры принимают во внимание перечисленные материалы при выборе компонентов для производства новых изделий. На основании собранных данных проводятся расчеты на прочность. Например, канаты, предназначенные для подъема и вытягивания, должны иметь запас прочности в десять раз больше их номинальной грузоподъемности. Регулярные проверки этих канатов осуществляются путем подвешивания груза, вес которого в десять раз превышает заявленную грузоподъемность каната.
Пределы прочности для критически важных конструкций имеют разные значения.
Сопротивления и модули упругости для строительных материалов
Таблица 1. Модуль упругости для основных строительных материалов.
Нормативные данные для вычислений железобетонных конструкций
Таблица 2. Коэффициенты упругости бетона (по данным СП 52-101-2003)
| Значения начального модуля упругости бетона при сжатии и растяжении Eb, МПа — 1 0-3, в зависимости от класса бетона по прочности на сжатие. | ||||||||||
| B10 | B15 | B20 | B25 | B30 | B35 | B40 | B45 | B50 | B55 | B60 |
| 19,0 | 24,0 | 27,5 | 30,0 | 32,5 | 34,5 | 36,0 | 37,0 | 38,0 | 39,0 | 39,5 |
Таблица 2.1 Показатель модуля упругости бетона в соответствии с СНиП 2.03.01-84* (1996)
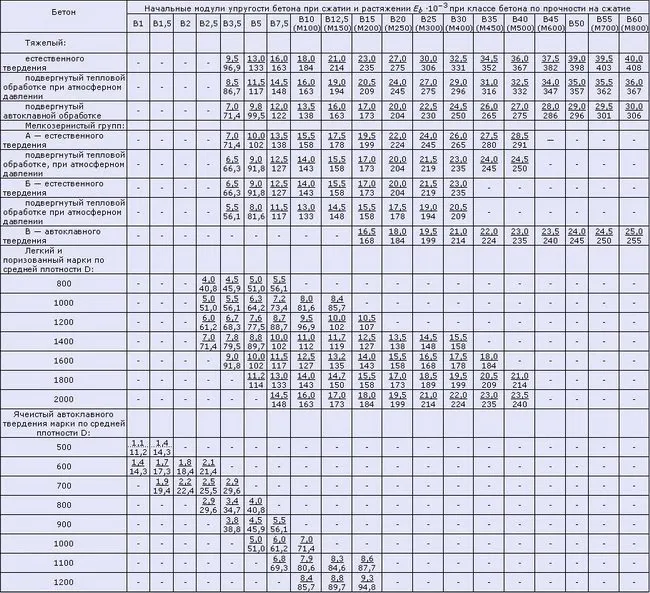
Примечания: 1. Над чертой указаны значения в мегапаскалях (МПа), под чертой — в килограмм-силах на квадратный сантиметр (кгс/см2). 2. Для легких, ячеистых и газобетонов с промежуточными значениями плотности бетона начальный модуль упругости рассчитывается методом линейной интерполяции. 3. Для газобетона, который не прошел автоклавную обработку, значения Eb устанавливаются аналогично автоклавному бетону, с применением коэффициента 0,8. 4. Для предварительно напряженного бетона значения Eb определяются как для тяжелого бетона, умноженные на коэффициент α.
Таблица 3: Обычные значения прочности бетона (по материалам СП 52-101-2003)
Таблица 4: Номинальные показатели прочности бетона на сжатие (по данным СП 52-101-2003)
Таблица 4.1 Значения проектной прочности бетона на сжатие в соответствии с СНиП 2.03.01-84* (1996)
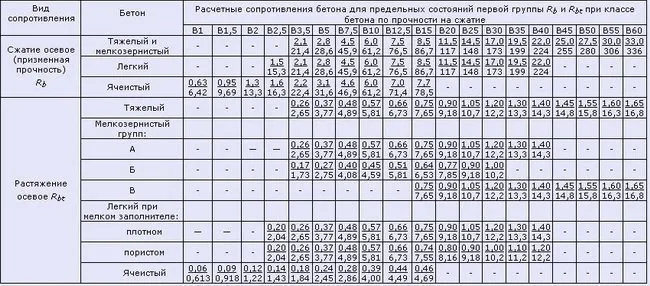
Таблица 5. Параметры для оценки прочности бетона на растяжение (в соответствии с СП 52-101-2003)
Таблица 6. Обычные значения прочности для армирующих изделий (согласно СП 52-101-2003)
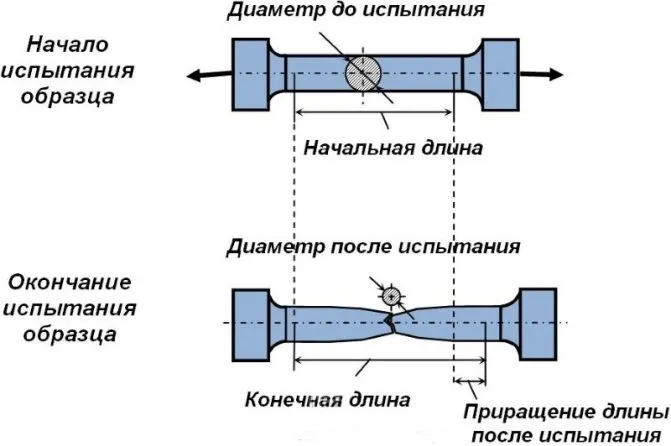
Таблица 6.1 Стандартные значения прочности для арматуры класса А в соответствии с СНиП 2.03.01-84* (1996)

Таблица 6.2 Стандартные значения прочности для арматуры классов В и К в соответствии с СНиП 2.03.01-84* (1996)
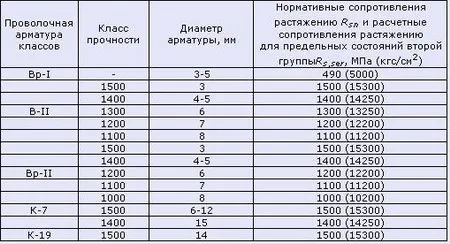
Таблица 7. Определение прочностных характеристик арматуры (в соответствии с СП 52-101-2003)
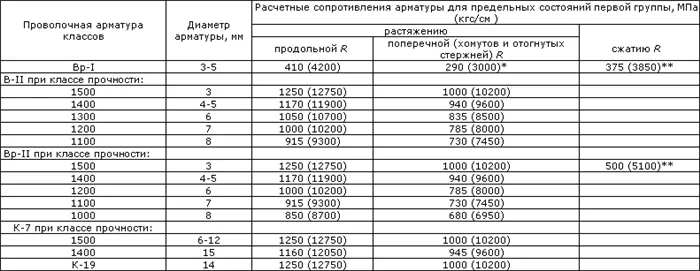
Таблица 7.1 Определение расчетного сопротивления арматуры класса А согласно СНиП 2.03.01-84* (1996)
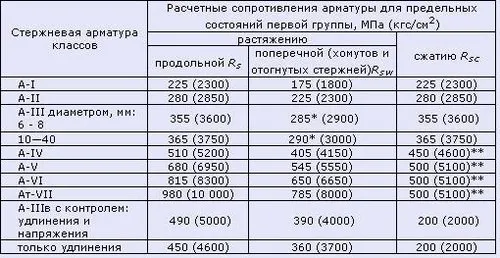
Таблица 7.2 Расчетные значения сопротивления для арматурных стержней марки В и К в соответствии с СНиП 2.03.01-84* (1996)
Нормативные данные для расчетов металлических контрукций
Таблица 8. Типовые и расчетные показатели прочности на растяжение, сжатие и изгиб (согласно СНиП II-23-81 (1990)) для стальных конструкций, изготовленных из листового металла, широкополосных изделий общего назначения и профилей, предназначенных для зданий и сооружений в соответствии с ГОСТ 27772-88.
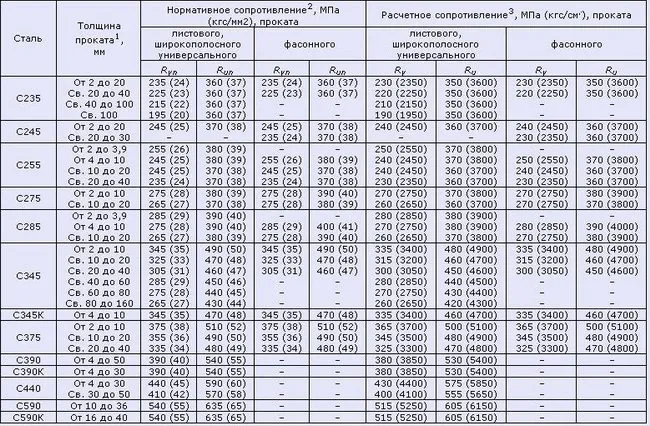
Примечания: 1. Толщина фасонных элементов должна определяться как толщина фланца (минимальное значение — 4 мм); 2. Нормативной прочностью считаются стандартные значения предела текучести и усталостной прочности согласно ГОСТ 27772-88; 3. Значения прочности конструкции вычисляются путем деления стандартных коэффициентов надежности материала, округленных до 5 МПа (50 кгс/см²).
Модуль упругости (Модуль Юнга)
Когда изделие из определённого материала подвергается влиянию определенной силы, оно начинает противостоять этому воздействию, будь то давление, растяжение или изгиб. Возможность сопротивляться такой нагрузке может быть оценена и выражена в математической форме. Эта характеристика прочности называется модулем упругости.
Данное значение изменяется в зависимости от типа материала и служит показателем его прочности. Эта характеристика применяется при разработке конструкций, элементов и различных изделий с целью избежать повреждения их структуры.

Например, усадка древесины архангельских бревен составляет 3-4%, кировских и вологодских — 4-6%, костромских — 6-7%, а тверских, смоленских и ярославских — до 10%. Поэтому при выборе материала для строительства дома следует обратить внимание на все эти факторы.
7 шагов для вычисления модуля упругости стали
Модуль упругости стали: определение, формула для расчета, прочность на разрыв и предельно допустимое механическое напряжение, а также шесть физических вспомогательных величин для технических расчетов упругости металлов. Кроме того, приведем инструкции по выполнению расчетов модуля упругости стали с использованием компьютера.

Вспомните свои школьные дни, когда вопрос «Где это будет полезно в жизни?» звучал практически в каждом классе. Для тех, кто имеет прямое отношение к металлургической отрасли, физика стала неотъемлемой частью их профессиональной деятельности.
Для создания качественной конструкции может быть недостаточно базовых знаний, и важно изучить более сложные аспекты. Модуль упругости стали – это один из важных параметров, который необходим конструкторам.
В данной статье мы подробнее рассмотрим, что собой представляет этот термин, как производится его расчет в контексте стали и другие важные аспекты данной темы.
Следует отметить, что модуль упругости Юнга не является постоянным значением. Даже для одного и того же типа стали его значение может изменяться в зависимости от местного приложения силы к объекту (хоть колебания и небольшие, они все-таки имеют место). Среди металлов только алюминий, сталь и медь обладают достаточно точными значениями этого параметра.

Пример, представленный выше, о строительных материалах взят из справочника, однако информация на бумаге не всегда может быть абсолютно точной. Рекомендуется использовать онлайн-калькуляторы или специальные программные решения для расчетов.
Как вычислить модуль упругости стали?
В сети легко найти онлайн-калькуляторы для выполнения таких расчетов. Мы выбрали один из лучших сайтов, который попал в топ поисковых систем. Вы можете ознакомиться с последними разработками по этой теме. http://www.stresscalc.ru/ex.php — перейдите на вкладку «Калькулятор», чтобы рассчитать модуль упругости для различных видов стали. Если у вас возникли сложности, просто посетите главную страничку и выберите кнопку, представленную на изображении ниже.


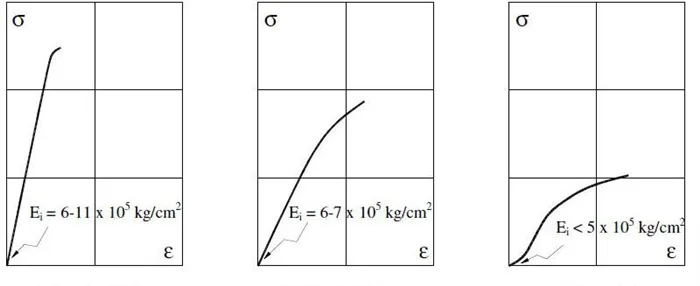
В данном разделе можно ознакомиться с символами. Все физические характеристики материалов основаны на данных ПНАЭ Г-7-002-86, а промежуточные значения расчетов модуля упругости стали получены с помощью линейной интерполяции.
Перед тем как применять представленную информацию на практике, необходимо сверить данные с ГОСТом. Неофициальные источники информации могут быть использованы лишь для предварительных расчетов или в простых конструкциях.
При строительстве крупных объектов следует несколько раз проверять модуль упругости, так как он влияет на прочность всей конструкции, учитывая выбранные элементы.