Вышеописанный закон Ома применим к весьма разнообразному набору металлов. Он продолжает действовать, пока металл не начнет плавиться. Однако в случае электролитических растворов и сильно ионизированных газов (плазмы) область его применения значительно сужается.
Закон Ома для полного и участка цепи: варианты записи формулы, описание и объяснение
Техник-электронщик и профессиональный электрик просто не могут обойтись без закона Ома в своей работе и сталкиваются с задачами, связанными с проектированием, наладкой и ремонтом электронных и электрических цепей.
На самом деле, каждый человек должен быть знаком с этим законом. В повседневной жизни нам часто приходится взаимодействовать с электричеством.
Несмотря на то, что в программе средней школы присутствует курс, посвященный закону немецкого физика Ома, на практике его изучение часто откладывается. В данной статье мы затронем важный аспект этого вопроса и рассмотрим различные способы написания текстов для газет.
Отдельный элемент и полная электрическая цепь
При анализе электрических схем с учетом закона Ома важно отметить два подхода к расчетам — один применим к отдельным компонентам, другой — к целым цепям.
Построение модели тока в цепи
Элемент цепи обычно рассматривается как часть общей схемы, где источник электромагнитной силы (ЭМС) исключается из-за добавленного внутреннего сопротивления.
В данном случае формула представляется достаточно простой.
Смысл формулы заключается в том, что ток, протекающий через данный элемент цепи, находится в прямой зависимости от напряжения, приложенного к нему, в то время как сопротивление является обратной величиной.
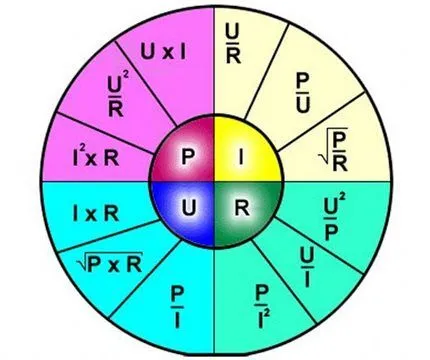
Представленная графическая «гирлянда» демонстрирует все аспекты формулы, основанной на законе Ома. Это удобные в эксплуатации карманные инструменты: сектор ‘P’ — мощность, сектор ‘U’ — напряжение, сектор ‘I’ — ток, сектор ‘R’ — сопротивление.
Таким образом, формула точно отображает зависимость тока, который проходит через определенный участок электрической цепи, от заданных значений напряжения и сопротивления.
К примеру, данную формулу целесообразно применять для вычисления сопротивления, которое вводится в цепь, принимая во внимание напряжение и ток.
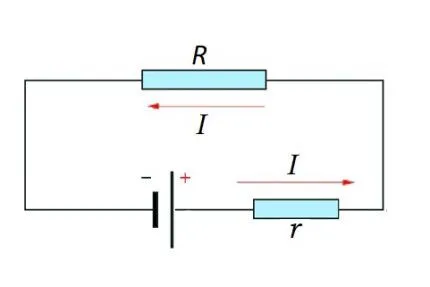
Закон Ома и его два основных следствия. Эта информация необходима всем профессиональным электрикам, инженерам в области электроники и другим специалистам, которые занимаются электрическими цепями. Слева направо: 1 — определение силы тока — 2 — определение сопротивления — 3 — определение напряжения. Здесь I обозначает ток, U — напряжение, а R — сопротивление.
Представленная выше схема позволяет вычислить, например, силу тока, проходящего через резистор с сопротивлением 10 Ом при приложенном напряжении в 12 вольт. Подставляя данные в формулу, мы находим: I = 12/10 = 1,2 ампера.
Аналогичным образом можно решить задачу по определению сопротивления (если известны ток и напряжение) или найти напряжение (если известны ток и сопротивление).
Следовательно, всегда есть возможность вычислить необходимое рабочее напряжение, требуемый ток и оптимальный резистивный элемент для конкретных условий.
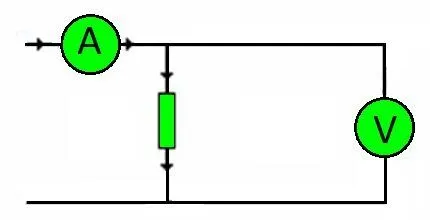
При обсуждении типов, доступных для применения, не следует учитывать параметры источника напряжения. Однако схемы, включающие, к примеру, батареи, требуют другого подхода к расчетам. На схеме: A — место подключения амперметра; V — место подключения вольтметра.
Важно отметить, что соединительные провода каждой цепи функционируют как резисторы. Объем нагрузки, которую они способны переносить, зависит от величины напряжения.
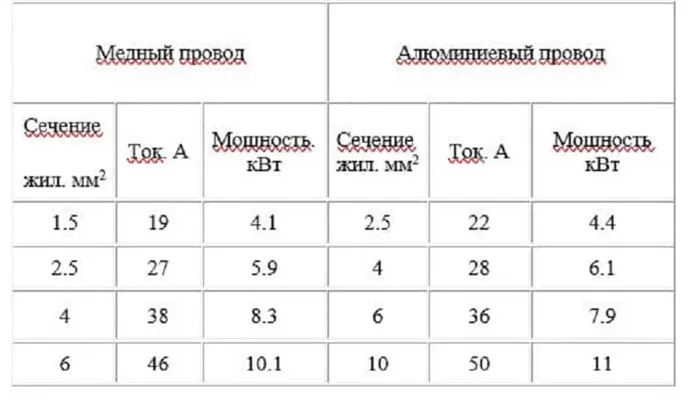
Поэтому, вновь обращаясь к закону Ома, выбор необходимого сечения проводника осуществляется с учетом материала сердечника.
На нашем сайте вы найдете подробные инструкции по расчету сечения кабеля в зависимости от мощности и тока.
Полные возможности расчета схемы
Полная схема в настоящее время включает в себя множество компонентов и источников ADR. Это значит, что на практике внутреннее сопротивление источника ЭМС добавляется к уже существующим антистатическим элементам в цепи.
Последовательное и параллельное соединение компонентов
Элементы схемы (части схемы) могут быть соединены либо последовательно, либо параллельно.
Каждый из этих типов подключения подразумевает различные характеристики подачи тока и напряжения. Таким образом, закон Ома применяется по-разному в зависимости от типа подключения.
Цепи антистатических элементов с последовательным соединением
Для последовательных соединений (часть цепи, содержащая два компонента) используется следующая терминология: «цепь антистатических элементов с последовательным соединением».
Данное выражение четко указывает на то, что ток, проходящий через определенный участок цепи, остается постоянным независимо от количества антистатических компонентов, подключенных последовательно.
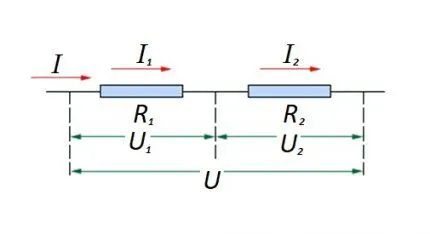
Антистатические элементы цепи соединены последовательно. Для такого случая используются различные методы расчета. На схеме: i, I1, I2 — токи, протекающие через элементы; r1, r2 — сопротивления элементов; u, u1, u2 — приложенные напряжения.
Сумма напряжений, приложенных к активным антистатическим компонентам схемы, составляет общее значение источника ADR.
Напряжение на каждом из концов каждого компонента определяется по формуле: Ux=I*Rx.
Общее сопротивление необходимо рассматривать как сумму всех номинальных значений антистатических элементов в цепи.
Цепь из антистатических элементов, соединенных параллельно
Для группы статических элементов, соединенных параллельно, справедливо применение немецкого закона Ома.
Применение параллельных и последовательных соединений не исключает возможности создания схемных компонентов «смешанного» типа.
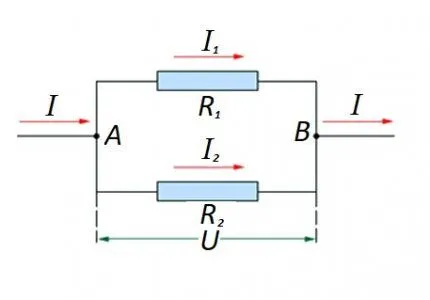
Резистивные компоненты в цепи соединяются параллельно, что требует особого подхода к расчетам. На схеме обозначены: I — общий ток, I1 и I2 — токи через резисторы R1 и R2 соответственно, U — напряжение, приложенное к цепи, A и B — точки подключения.
При выполнении расчетов обычно сначала определяют эквивалентное сопротивление для параллельного соединения резисторов, а затем добавляют к нему значение последовательного сопротивления для получения общего результата.
Интегральная и дифференциальная формы закона
Указанные методы расчетов применимы в случаях, когда в электрической цепи используются проводники, обладающие «однородной» конструкцией.
На практике часто возникают ситуации, где структура проводников варьируется в зависимости от разных областей. К примеру, могут применяться провода с увеличенной площадью поперечного сечения или, наоборот, с уменьшенной площадью и изготовленные из различных материалов.
Для учета этих различий существует метод, известный как «омический дифференциально-интегральный подход». В случае небольших проводников плотность тока определяется как функция от напряжения и проводимости материала.
Дифференциальные расчеты осуществляются по формуле: J=ό*E
Для вычисления интегралов используется уравнение: I *R=φ1-φ2+έ
Тем не менее, эти примеры достаточно близки к высшей математике и не имеют практического применения для повседневной работы электрика.
Чаще всего подразумевается, что внутреннее сопротивление источника тока сравнительно невелико относительно сопротивления внешней цепи. В таких случаях закон Ома применяется к замкнутой цепи с формулой I = U/R.
Формулировки и основные формулы
Закон Ома формулируется так: ток, протекающий через проводник, прямо пропорционален напряжению, приложенному к концам проводника, и обратно пропорционален его сопротивлению.
- С увеличением напряжения на проводнике возрастает и ток в этом проводнике.
- С увеличением сопротивления проводника ток в нем уменьшается.
Основные параметры, описывающие электрические цепи, известны многим из школьного курса физики.
Пояснение закона Ома в классической теории
Формула закона, известная всем еще с начальной школы, выглядит следующим образом:
С ее помощью можно легко вывести уравнение для выявления UU.
Единицей измерения тока является ампер, напряжение – вольт, а сопротивление – ом.
Этот закон применяется к линейной части схемы, где сопротивление остается постоянным.
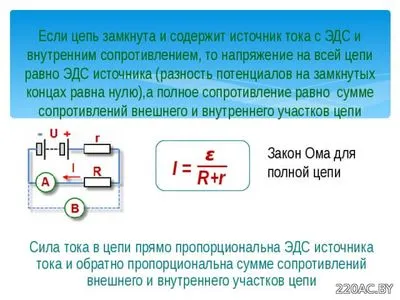
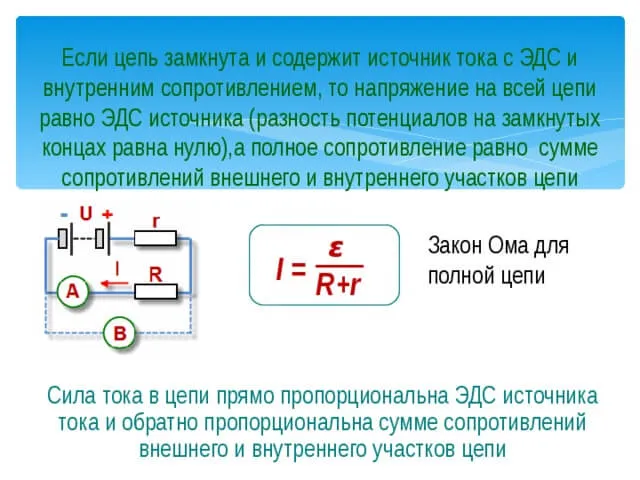
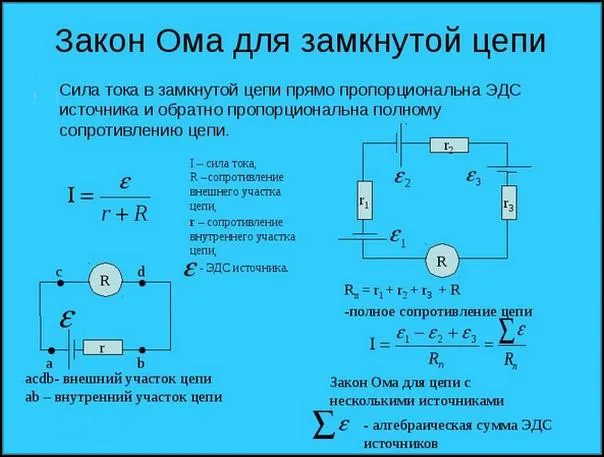
Закон Ома для полной (замкнутой) цепи
Замкнутая или полная цепь — это цепь, через которую протекает электрический ток.
Уравнение для представленной полной цепи можно записать как:
где ϵ обозначает электродвижущую силу или напряжение источника питания, которое не зависит от внешней цепи.
R – сопротивление внешней цепи.
r – внутреннее сопротивление источника питания.
Обратите внимание, что в ходе эксперимента напряжение на конце используемого проводника должно оставаться неизменным. Это значение не должно колебаться, чтобы корректно оценить зависимость тока от сопротивления.
Пояснение закона Ома в классической теории
Формула закона, известная еще со школьных времен, выглядит следующим образом:
Из данной формулы можно легко извлечь уравнение для определения напряжения (U).
Единица измерения тока — ампер, напряжения — вольт, а сопротивления — ом.
Этот закон актуален для линейной части электрической цепи с постоянным сопротивлением.
Закон Ома для полной (замкнутой) цепи
Полная или замкнутая цепь — это такая цепь, по которой протекает электрический ток.
Уравнение для полной электрической цепи записывается как
где ⌘ (эпсилон) обозначает электродвижущую силу или напряжение источника, которое не зависит от нагрузки внешней цепи.
R — сопротивление внешней цепи, а
r — внутреннее сопротивление источника питания.
Применение закона Ома для параллельного и последовательного соединения
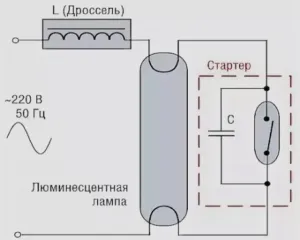
При последовательном соединении элементы цепи располагаются друг за другом. Поскольку это простая электрическая цепь, ток будет одинаковым на каждом участке. Ярким примером последовательного соединения служат лампы в рождественских гирляндах.
Когда элементы соединены последовательно, основные параметры электрической цепи могут быть вычислены следующим образом:
Обозначим ˉ(I \) как общий ток в электрической цепи, ˉ(I_1 \) – ток в первой ветке, ˉ(I_2 \) – ток во второй ветке, а ω(I_3 \) – ток в третьей ветке.
Пусть \(U \) представляет общую напряжение, \(U_1 \) – напряжение на первой позиции, \(U_2 \) – напряжение на второй позиции и \(U_3 \) – напряжение на третьей позиции.
Пусть \(R \) обозначает общее сопротивление цепи, \(R_1 \) – сопротивление первой ветки, \(R_2 \) – сопротивление второй ветки и \(R_3 \) – сопротивление третьей ветки.
Параллельное соединение элементов создает разветвленную электрическую цепь. Примером такого типа соединения служит стандартная электропроводка в жилых помещениях. Благодаря этому можно одновременно включать несколько электроприборов и осветительных устройств в одном помещении.
Когда компоненты располагаются параллельно, основные электрические параметры цепи рассчитываются следующим образом:
Где I — это общий ток в электрической цепи, а I_1, I_2, I_3 — токи в первой, второй и третьей секциях соответственно.
Где U — общее напряжение, а U_1, U_2, U_3 — напряжения в секциях 1, 2 и 3 соответственно.
Здесь R — общее сопротивление цепи, а R_1, R_2, R_3 — сопротивления первой, второй и третьей частей цепи соответственно.
Несомненно, закон Ома предполагает, что внутреннее сопротивление АДР в полной электрической цепи можно считать незначительным. Однако значение этого сопротивления сильно зависит от конструкции источника АДР.
Сопротивление источника тока
Закон Ома для полных электрических цепей, а также уравнения для вычисления их параметров описывают не только ток, протекающий через цепь, но и характеристики, которые присутствуют внутри источника. При анализе отдельных частей цепи закон Ома не учитывает эти величины.
Батареи способствуют перемещению электронов от положительного электрода к отрицательному. В рамках электрической цепи электроны постоянно движутся в обратную сторону. Уменьшение числа электронов на отрицательной клемме и их увеличение на положительной клемме всегда компенсируется процессами, происходящими внутри устройства.
Это движение электронов классифицируется как электрический ток. Частицы должны преодолевать внутреннее сопротивление источника тока. Характер изменений зависит от конкретного материала, так как сопротивление может варьироваться при изменении температуры.
Цепи переменного тока обладают как активным, так и реактивным сопротивлением. Первое из них было определено ещё в работах Джорджа Ома. Однако индуктивные и емкостные компоненты также создают препятствия для движения электронов. Таким образом, закон Ома применим и к переменному току.
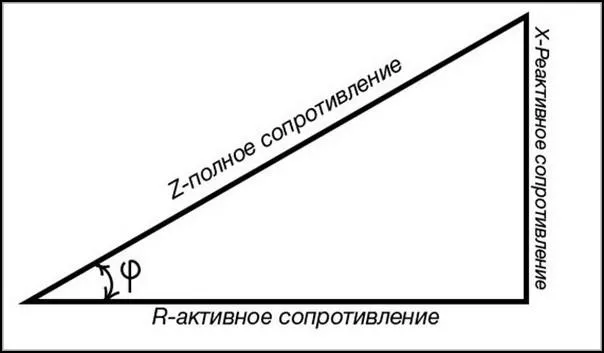
Для корректного применения этого закона в таких цепях необходимо учитывать полное сопротивление, которое включает в себя влияние как активных, так и реактивных компонентов резисторов.
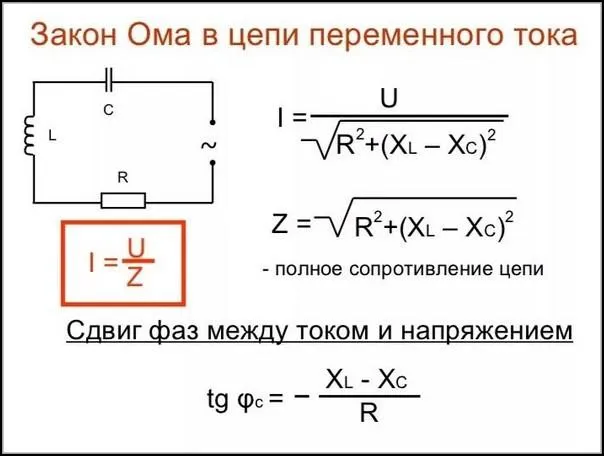
На схеме, представленной на рисунке, импеданс обозначается как Z. Омическое, индуктивное и емкостное сопротивления соответственно равны R, XL и XC. Закон Ома для цепей переменного тока учитывает все эти виды сопротивлений. Из данной формулы следует, что сложение резисторов происходит по векторному правилу.
Для вычисления всех типов сопротивлений применяется прямоугольный треугольник: один катет отражает активное сопротивление, а другой — реактивное. Реактивное сопротивление равно разности между индуктивным и емкостным сопротивлениями. Эта величина определяется согласно теореме Пифагора, которая утверждает, что длина диагонали равна квадратному корню из суммы квадратов двух перпендикулярных сторон.