Последовательность Фибоначчи и золотое сечение оказывают значительное влияние на физику и законы природы:
Поиск золотой середины, или тайны золотого сечения
Число φ (фи), известное как золотое сечение или средняя величина, представляет собой одно из самых таинственных понятий в математике и физике. Удивительно, но оно часто встречается в нашем повседневном окружении, хотя многие люди этого даже не осознают. Даже те, кто не знаком с концепцией золотого сечения, могут столкнуться с ним без ведома об этом. Проведенные исследования показывают: участникам демонстрируют случайные лица и просят определить наиболее привлекательные. Оказалось, что эти лица обладали золотой пропорцией между различными характеристиками — шириной лица, расстоянием между глазами, линией бровей и носом. Таким образом, люди инстинктивно воспринимают приближенность к тем пропорциям, которые считаются идеальными.
Это пропорция, полученная методом деления в крайних и средних величинах. Этот процесс также известен как гармоническое деление. Как же вычисляется золотая середина? В математических терминах эта величина представляет собой соотношение двух значений a и b, где выполняется условие: a > b, а также соблюдается следующее уравнение: a/b = (a + b)/a. Установив, что a и b являются частями одной целого, можно заключить, что отношение меньшей части к большей эквивалентно отношению большей части к всему целому. Золотое сечение обозначается 21-й буквой греческого алфавита — Φ (читается как фи).
Как и число π, это число является бесконечным и устанавливает соотношение между окружностью круга и его диаметром. Оно записывается так: 1.6180339887498948420…. Поэтому оно обычно округляется до 1,618.
История золотого сечения
Это значение известно под несколькими названиями, такими как божественное соотношение и асимметричная симметрия. Считается, что метод золотого сечения был введен в науку Пифагором в 6 веке до нашей эры. Уточняется, что он познал этот метод благодаря египтянам и вавилонянам. Доказательством использования аналогии золотого сечения служат пропорции пирамид, храмов, рельефов, а также различных предметов быта и украшений.
Это правило можно наблюдать и в другой древней архитектуре. К примеру, высота пирамиды Гизы составляет 146,6 метра, а длина каждой стороны основания равна 230,5 метра. Если рассчитать отношение длины стороны к высоте, мы получим 1,5717, что очень близко к числовому значению F. Греческий скульптор и математик Фидий, живший в пятом веке до нашей эры, использовал принцип золотого сечения при создании своих скульптур для Парфенона. Платон называл золотое сечение универсальной основой математических соотношений. Евклид также заметил присутствие золотого деления в конструкции пентаграммы еще в IV веке до нашей эры.
Последовательность Фибоначчи занимает важное место в данной концепции. Известный математик сформировал ряд чисел, где если взять любые два соседних элемента, их отношение оказывается очень близким к Золотому сечению (обозначаемому как F). С увеличением чисел это соотношение всё более приближается к 1,618. К примеру, при рассмотрении чисел 3 и 5 мы получаем отношение 1,666, а для чисел 13 и 21 – значение 1,625. При равном значении F соотношение составляет 144 к 233.
«Золотые» фигуры
Принцип золотого сечения активно применяется при создании геометрических фигур. Считается, что такие фигуры выглядят более эстетично и привлекательнее. Это подтверждено множеством экспериментов, показывающих, что внимание людей больше фокусируется на фигурах, основанных на этом принципе.

Примером, который легко понять, является прямоугольник, соотношение сторон которого позволяет вычислить значение F. Другим удачным примером служит правильный пятиугольник. Все диагонали этого многоугольника делят друг друга на отрезки, которые соответствуют золотому сечению, и каждый из концов образует золотой треугольник. В вершине такого треугольника образуется угол в 36 градусов, а основание делит одну из сторон в соответствии с золотым сечением. Внутри пятиугольника можно построить пентаграмму.
Древнегреческий ученый Архимед первым пояснил, что изящная спираль возникает при вырезании из золотого прямоугольника одного квадрата и соединении противоположных углов с помощью четверти окружности.
Всемогущий Творец установил для каждого из своих созданий определенные пропорции и гармонию, что находит подтверждение в примерах природного мира. Существует множество случаев, когда рост живых организмов точно соответствует форме логарифмической спирали.
История открытия золотой середины
Это число много раз подсчитывали и изучали, поэтому у него существует множество наименований, включая золотое сечение, золотая пропорция и божественное сечение. На протяжении истории оно использовалось в архитектуре различных древних сооружений, таких как Великие пирамиды и Парфенон. Например, у пирамиды Гизы длина каждой стороны основания равна 230,5 м, а высота составляет 146,6 м. Соотношение между основанием и высотой примерно равно 1,5717, что близко к золотому сечению.
Фидий (около 500 года до н. э. — примерно 432 год до н. э.) был выдающимся греческим скульптором и математиком, который, как предполагается, использовал золотое сечение при создании знаменитых скульптур Парфенона. Платон (428 год до н. э. — 347 год до н. э.) утверждал, что золотое сечение представляет собой наиболее универсальную пропорцию в математических соотношениях. В дальнейшем Еклид (365 год до н. э. — 300 год до н. э.) связал золотое сечение с конструированием пентаграммы.
Последовательность Фибоначчи и золотое сечение
Примерно в 1200 году математик Леонардо Фибоначчи изучил необычные свойства последовательности, ныне известной как последовательность Фибоначчи. Эта числовая последовательность тесно связана с концепцией золотого сечения. Если рассмотреть два последовательных числа из этой последовательности, то отношение между ними будет очень близко к значению золотого сечения. С увеличением чисел это соотношение стремится к 1,618. Например, отношение 3 к 5 составляет 1,666, тогда как отношение 13 к 21 равно 1,625. При сравнении 144 и 233 мы видим, что их отношение всё более приближается к 1,618. Все указанные числа являются последовательными элементами последовательности Фибоначчи.
Соотношения из последовательности Фибоначчи, которые приближают значение золотого сечения, могут быть использованы для создания пропорций прямоугольника, известного как золотой прямоугольник. Этот прямоугольник считается одной из самых эстетически совершенных геометрических фигур, что и объясняет широкое применение правила золотого сечения в различных формах изобразительного искусства. Золотой прямоугольник также ассоциируется с золотой спиралью, формируемой за счет соединения квадратов, размеры которых соответствуют числам Фибоначчи.
Пропорции золотого сечения в материальном мире
В 1509 году Лука Пачоли опубликовал труды, в которых он обозначил число F как «Божественную аналогию», графическая иллюстрация которой была создана Леонардо да Винчи. Позже да Винчи обобщил это соотношение под названием золотое сечение. Оно использовалось во многих произведениях живописи и скульптуры эпохи Возрождения для достижения гармонии и красоты.
Леонардо да Винчи применял золотое сечение для расчета всех пропорций в «Тайной вечере», включая размеры стола, отношения стен и детали интерьера. Золотое сечение также можно обнаружить в «Витрувианском человеке» и «Моне Лизе». Считается, что этот принцип использовали и другие знаменитые художники, такие как Микеланджело, Рафаэль, Рембрандт, Сера и Сальвадор Дали.
Термин «фи» был представлен американским математиком Марком Барром в начале двадцатого века. Концепция продолжила свою жизнь в математике и физике, в том числе благодаря плитке Пенроуза, разработанной в 1970-х годах, которая создала возможность пятой симметрии мозаичных поверхностей. В восьмидесятых годах F появилась в квантовых кристаллах, новой форме материи, недавно открытой учеными.
Фи — это не просто загадочный термин, который можно встретить в математике и физике. Он присутствует повсюду в нашей повседневной жизни, включая наше восприятие красоты. Научные исследования показали, что люди, оценивающие случайные лица, чаще всего считают наиболее привлекательными те, которые демонстрируют явные пропорции, схожие с золотым сечением. Особенно ярко это выражается в гармонии между шириной лица и расстоянием между глазами, носом и бровями. При этом испытуемые не были профессионалами в математике или физике и зачастую не имели представления о правиле золотого сечения — они были простыми людьми, реагирующими на визуальные стимулы инстинктивно.
Золотое сечение также присутствует во множестве аспектов природы и науки. Рассмотрим примеры его удивительного проявления в различных областях.
- Лепестки. Число лепестков у некоторых растений совпадает с последовательностью Фибоначчи. Согласно дарвиновской теории, каждый лепесток расположен таким образом, чтобы максимально эффективно получать солнечное освещение и учитывать другие окружающие факторы.
- Семенные головки. Процесс формирования семян в цветке зачастую начинается в центре семенной головки и постепенно продвигается наружу, заполняя свободные пространства. Например, семена подсолнечника следуют указанной схеме.
- Сосновые шишки. Внутри сосновых шишек находятся семена, которые расположены по спирали, поднимаясь в противоположных направлениях. Как правило, количество витков спиралей соответствует числам Фибоначчи.
- Ветви дерева. Формирование или разветвление древесных ветвей служит ярким примером выполнения закономерностей последовательности Фибоначчи. Подобные схемы также можно наблюдать в корневых системах растений и водорослях.
- Моллюски. Многие раковины, такие как улитки и наутилусы, великолепно иллюстрируют концепцию золотой спирали.
- Спиральные галактики. Галактика Млечный Путь включает несколько спиральных рукавов, каждый из которых имеет логарифмическую спираль с углом приблизительно 12 градусов. Структура спирали схожа с золотой спиралью, и над каждой спиральной галактикой можно провести золотой прямоугольник.
- Ураганы. Внутренняя архитектура ураганов часто следует принципам золотой спирали.
- Пальцы рук человека. Длина каждой части пальца от кончика до запястья увеличивается примерно в F раз по сравнению с предыдущей частью.
- Тела людей и животных. Промежуток между пупком человека и землей, а также расстояние от макушки головы до пупка составляют золотое сечение. Однако люди не единственные представители животного мира, где встречается этот принцип. Дельфины, морские звезды, морские ежи, муравьи и пчелы тоже иллюстрируют подобные пропорции.
- Молекулы ДНК. Размеры молекулы ДНК составляют 34 ангстрема на 21 ангстрем в каждом полном витке двойной спирали. Числа 34 и 21 являются последовательными в ряду Фибоначчи.
Узнаем, что объединяет древнеегипетские пирамиды, «Монну Лизу» Леонардо да Винчи, подсолнух, улитку, сосновую шишку и человеческий палец.
См. также
- ↑ ^ Радзюкевич А.В. Золотое сечение: Красивая история
- ↑ ^ Марио Ливио, Золотое сечение: История Фи, самого удивительного числа на свете.
- ↑ ^ Уголок Девлина, миф, который продолжает существовать
- ↑ ^ Золотая акция: архитектурное наследие
- Бендукидзе А. Д. Золотое сечение «Квант» № 8, 1973 год.
- Васютинский Н. А. Золотое сечение — М.: Молодая гвардия, 1990 — 2382 страницы.
- Шмигевский Н. В. Формула совершенства // Страна знаний — 2010 — № 4 — С. 2-7.
- Сабанеев Л. Л. Этюды Шопена для объяснения закона золотого сечения. Опыт позитивного силлогизма законов формы // Искусство. 1925 — № 2 — С. 132-145; 1927 — № 2-3 — С. 32-56.
Ссылки
- Числа с названиями
- Золотое сечение
- Алгебраические числа
Фонд Викимедиа. 2010.
Полезные ресурсы
Смотрите, что такое «Золотое сечение» в других словарях:
ЗОЛОТОЕ СЕЧЕНИЕ — это математическое отношение, которое также называют золотым сечением, крайним и средним делением или гармоническим делением. Оно представляет собой деление отрезка AC на две части так, что большая часть AB соотносится с меньшей частью BC так же, как весь отрезок AC соотносится с большой частью AB. То есть выполняется соотношение: AB : BC = AC : AB. Это понятие имеет широкое применение в различных областях науки и искусства, включая архитектуру и живопись.
ЗОЛОТОЕ СЕЧЕНИЕ — это понятие, относящееся к гармоническому делению, при котором отрезок AS разделяется на две части таким образом, что большая часть AB соотносится с меньшей частью BC так, как весь отрезок AS сопоставляется с AB (т.е. AB:BC = AS:AB). Это принцип деления также активно используется в искусстве и архитектуре для достижения эстетической гармонии.
Золотое сечение, известное также как крайнее и среднее деление или гармоническое деление, представляет собой метод деления отрезка AS на две части, где большая часть AB пропорциональна меньшей части BC аналогично тому, как весь отрезок AS пропорционален части AB (то есть AB:BC = AS:AB).
Термин Золотое Сечение (Golden Section) определяется как деление отрезка AC на две составляющие, в которых большая часть AB сопоставима с меньшей частью BC таким же образом, как весь отрезок AC сравнивается с AB (например, AB:BC=AC:AB). Этот концепт часто применяется в различных областях, таких как живопись, архитектура и дизайн, поскольку он способствует созданию визуально привлекательных композиций.
Золотое сечение, также известное как гармоническое деление, пропорция или число Фидия, представляет собой принцип, применяемый для достижения идеальных пропорций и гармонии в архитектуре. Этот концепт используется с древних времён для нахождения наиболее привлекательного соотношения между элементами зданий или архитектурных сооружений. Суть золотого сечения заключается в делении целого на две неравные части, где отношение большей части к меньшей равно отношению целого к большей части.
ЗОЛОТЕ СЕКЦИИ — необходимо обратиться к работе Фехнера Г. Т. «Большой психологический словарь». Москва: Премьер-министр. Под редакцией Б.Г. Мещерякова и академика В.П. Зинченко, 2003 год … Это источник содержащий важную информацию в области психологии.
Золотое сечение также рассматривается в контексте информационных технологий — см. Л. Г. Суменко. «Англо-русский словарь по информационным технологиям». Москва: Государственный университет науки и технологий, 2003 год. Этот свод знаний охватывает темы, связанные с золотым сечением в рамках информационных технологий…. По материалам L.G. — Руководство для технических переводчиков.
Золотое сечение представляет собой способ деления отрезка или области на части так, что отношение меньшего участка к большему такое же, как отношение большего участка ко всему отрезку или области. В более простых терминах это можно выразить через дробь 21/34 (приблизительно 0,618) … Словарь-справочник версий
Золотое сечение (также известное как золотая пропорция, крайнее и среднее деление, гармоническое деление) — это процесс разделения отрезка на две части таким образом, что длина всего отрезка соотносится с большей из двух частей, аналогично тому, как большая часть относится к меньшей. Уравнение золотого сечения … Большая техническая энциклопедия
Леонардо да Винчи уделил значительное внимание изучению особенностей золотого сечения, и есть предположение, что этот термин может быть связан с его работами. Его чертежи стереометрических объектов, построенных на основе правильных пятиугольников, показывают, что каждый из прямоугольников, возникающих в результате сечений, соблюдает соотношение сторон, характерное для золотого сечения.
Золотая пропорция в анатомии легких человека
В своих научных исследованиях по физике и анатомии американский физик Б.Д. Вест и доктор А.Л. Голдбергер обнаружили, что золотое сечение присутствует и в строении человеческих легких.
Одной из ключевых особенностей бронхов, образующих легкие человека, является их асимметрия. Бронхи состоят из двух главных дыхательных путей: один (левый) значительно длиннее, чем другой (правый), который короче.
* Исследования показали, что асимметрия сохраняется не только в ветвях бронхов, но и во всех мелких дыхательных путях. Соотношение между длинами коротких и длинных бронхов также соответствует золотому сечению, равному 1:1.618.
Структура золотого ортогонального четырехугольника и спирали
Золотое сечение — это особый способ деления отрезка на неравные части, при котором весь отрезок соотносится с большей частью так же, как эта большая часть соотносится с меньшей; иными словами, меньшая часть относится к большей так, как большая часть относится к целой.
В геометрии прямоугольник с данным соотношением сторон называется золотым прямоугольником. Соотношение длин длинных и коротких сторон составляет 1.618 : 1.
Золотой прямоугольник известен своими замечательными характеристиками. Если из золотого прямоугольника вырезать квадрат с одной стороной, которая равна короткой стороне прямоугольника, сформируется новый золотой прямоугольник, но меньшего размера. Этот процесс может продолжаться до бесконечности. Продолжая вырезать квадраты, мы получаем всё меньшие золотые прямоугольники, которые также содержат логарифмическую спираль. Это важно для математических моделей физических объектов, например, раковин улиток.
Центр спирали расположен в точке пересечения диагоналей исходного прямоугольника и первой линии, проведенной перпендикулярно. Кроме того, диагонали всех следующих уменьшающихся золотых прямоугольников будут находиться на этих же диагоналях. Не забываем также о существовании золотого треугольника.
Английский дизайнер и эстетик Уильям Чарльтон подчеркивает, что спиральные формы оказывают привлекательное воздействие на зрение людей и используются ими на протяжении тысячелетий. Он объясняет это следующим образом:
«Нам нравится вид спирали, потому что он легок для визуального восприятия.»
В природе
* Принцип золотого сечения, который применяется к спиральной форме, регулярно встречается в природных образцах, обладающих исключительно красивым видом. Наиболее яркие примеры включают спиральные структуры, наблюдаемые в расположении семян подсолнечника, сосновых шишках, ананасах, кактусах, а также в архитектуре лепестков роз и т.д.

* Учёные-ботаники выяснили, что в организации расположения листьев на ветвях, а также семян подсолнечника и сосновых шишек можно наблюдать иерархию последовательности Фибоначчи, что, в свою очередь, иллюстрирует принцип золотого сечения.
Всемогущий Творец установил уникальные параметры для каждого своего создания, придав им пропорциональность, что можно увидеть на многих примерах в природе. Существует множество случаев, когда рост живых организмов строго соответствует конфигурации логарифмической спирали.
Все витки этой спирали имеют одинаковую структуру. Исследования математиков показали, что форма спирали остаётся неизменной даже при масштабировании её размеров. В математической науке нет другой фигуры, которая обладала бы аналогичными исключительными свойствами, как спираль.
Дизайнеры и кутюрье основывают свои расчеты на принципах золотого сечения. Человеческая фигура служит универсальным образцом для оценки этих пропорций. Однако не все люди обладают идеальными пропорциями от природы, что иногда затрудняет выбор одежды.
Божественная гармония золотого сечения в архитектуре: фотографии древних сооружений и примеры современного строительства
Множество сохранившихся до нашего времени древних строений демонстрирует, что они были возведены с учетом правил идеальной пропорции. Это могут быть королевские резиденции, церкви и общественные здания. Рассмотрим, например, применение принципа золотого сечения в различных странах.
Тайны древнеегипетской архитектуры
В архитектуре Древнего Египта пирамида Хеопса была возведена в соответствии с принципами золотого сечения. Наблюдая за работой строителей, можно заметить правильный треугольник, где одна сторона представляет собой высоту, а другая — половину длины основания. Если взять отношение гипотенузы к более короткой стороне, то мы получаем идеальное значение 1,61950 или приблизительно 1,62.
Это любопытно! Форма пирамиды обладает еще одним удивительным свойством. Структуры внутри нее становятся прочнее, вода дольше сохраняет свежесть, а растения начинают расти быстрее. Ученые уже на протяжении долгого времени пытаются понять этот феномен, однако научного объяснения до сих пор не найдено.
Существуют исследования, подтверждающие, что пирамида способствует улучшению психоэмоционального состояния людей, уменьшает вредное излучение в своем окружении и устраняет геопатогенные зоны.

Совершенная пропорция золотого сечения в пирамиде
Идеальные соотношения в Древней Греции
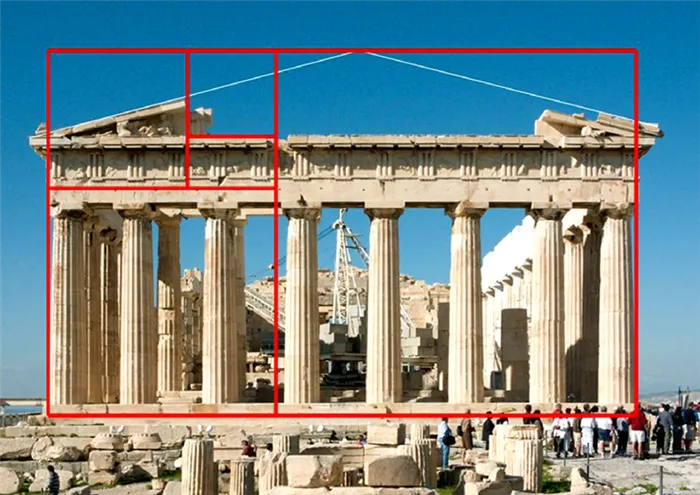
Совершенная пропорция придаёт архитектурным сооружениям неповторимость. Ярким примером золотого сечения из древнегреческой архитектуры является Парфенон, возведённый в 5 веке до нашей эры. Если рассмотреть соотношение высоты к ширине, то можно получить почти идеальное значение 0,618.
Исследователи установили, что для достижения истинного золотого числа необходимо вычесть 14 сантиметров из высоты и добавить это количество к ширине. Учитывая особенности конструкции здания, есть вероятность, что такие изменения были преднамеренно внесены древними архитекторами Иктиноном и Калликратом, поскольку фасад немного сужается вверх и отклоняется от золотого прямоугольника. Тем не менее, общие пропорции золотого сечения соблюдаются.
Принципы идеальной пропорции в древнегреческом Парфеноне:

Памятники архитектуры средневековья
Собор Нотр-Дам в Париже — великолепный образец средневековой архитектуры, успешно дошедший до нашего времени.

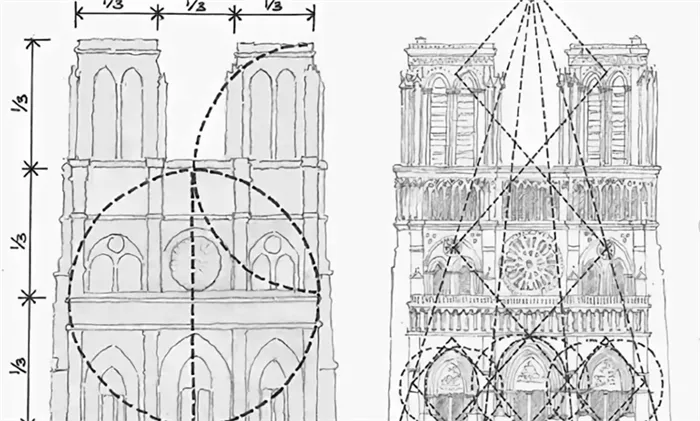
При исследовании структуры принципа СК можно обнаружить его применение в различных аспектах.
Архитектура России
Числа Фибоначчи представляют собой своего рода средство, которое можно применять для анализа архитектурных объектов. Для более удобной навигации круг Фибоначчи можно организовать, основываясь на принципе золотого сечения.
Правило золотого сечения при проектировании частного дома
Множество архитекторов, занимающихся разработкой проектов частных домов, применяют концепцию «золотого сечения». Заказчики ощущают, что каждая деталь продумана для обеспечения максимального комфорта проживания. При правильном распределении пространств жильцы испытывают чувство гармонии и умиротворения на психологическом уровне.
Что нужно учитывать при проектировании фасада
В современном строительстве, помимо чисел Фибоначчи, применяется еще один метод, инициатором которого стал французский архитектор Ле Корбюзье. Он основывался на росте предполагаемых владельцев жилья и на этой основе определял размеры строения и пространств внутри него. Такой подход позволил создать дом, который оказался не только гармоничным, но и исключительно удобным, учитывающим индивидуальные особенности жильцов.
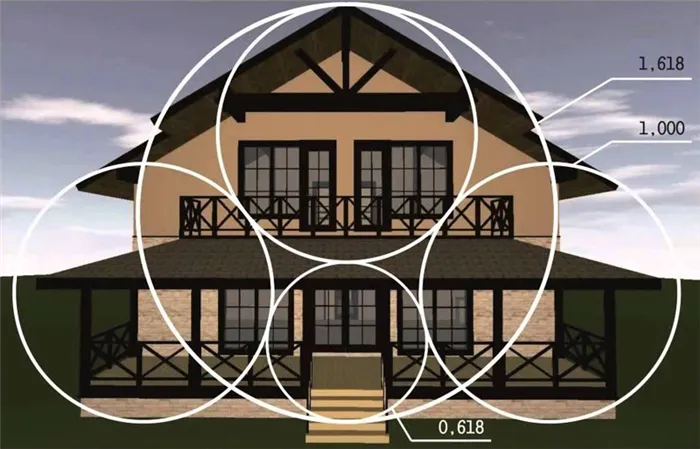
Идеальные пропорции для отдельно стоящего дома
Золотое сечение в дизайне интерьера
Даже если ваше жилье возведено по стандартному проекту, возможно создать интерьер, который максимально соответствует идеальному соотношению 1:1,62. К примеру, можно установить дополнительные перегородки или организовать мебель в группы, а также изменить размеры дверных и оконных проемов, чтобы достичь золотого баланса между шириной и высотой.
Аналогичным образом работает упрощенное правило и в выборе цветовой палитры интерьеров:
- 60% — основная цветовая гамма,
- 30% — дополнительный цвет,
- 10% — акцентный цвет, подчеркивающий восприятие основных и дополнительных оттенков.
Принцип 1/1,62 в дизайне интерьера должен соблюдаться во всех аспектах: соотношение мебели к общей площади помещения, а также высота предметов относительно параметров комнаты.



Заключение
Принцип золотого сечения имеет давние корни в архитектуре, поскольку ранее здания создавались не по унифицированным шаблонам, а соответствовали индивидуальным характеристикам владельцев. Такие постройки продолжают выглядеть гармонично и привлекательно спустя много лет. Интерьеры с идеальными пропорциями позволяют эффективно использовать доступное пространство.
Теперь у вас есть возможность самостоятельно и правильно применять божественную гармонию чисел при планировании строительства вашего дома или оформлении интерьера. Кроме того, интересная комбинация чисел может быть использована в области финансов, инвестиционных расчетах и во всех аспектах вашей повседневной жизни.
Если у вас остались вопросы, предлагаем ознакомиться с видео, в котором доступным языком разъясняется принцип золотого сечения:
В геометрии прямоугольник с таким соотношением сторон называется золотым прямоугольником. Соотношение длинных и коротких сторон составляет приблизительно 1,618 : 1.
Причины популярности золотого сечения
Интерес к этой теме впервые проявил М. Ливио. Золотое сечение: история числа PHI, одного из самых удивительных чисел в мире, берет начало от древнегреческих математиков Пифагора и Евклида. Они верили, что вся Вселенная устроена на основе чисел, которые можно применять для объяснения любых процессов. Не вызывает удивления тот факт, что такая элегантная идея привлекла внимание древних философов.
С тех пор золотое сечение стало объектом изучения многих выдающихся учёных и художников, таких как Леонардо да Винчи, Альбрехт Дюрер, Иоганн Кеплер, Ле Корбюзье, Сальвадор Дали и Ричард Пенроуз.
Его считают «божественной пропорцией»
Термин «золотое сечение» был введен немецким математиком Мартином Омом в XIX веке. Ранее эта концепция была известна как «божественная пропорция», согласно С. Строгацу и материалам, опубликованным в The New York Times Opinionator.
Благодаря приписываемым ему уникальным качествам золотое сечение стало широко применяться в разных сферах. В эпоху Возрождения эта геометрическая форма считалась идеальной для определения пропорций. Например, «золотой прямоугольник» часто использовался в дизайне книг и произведений искусства. Кроме того, талию человека называли пределом золотого сечения его физической формы.
Даже в современном мире некоторые люди рассматривают это соотношение как ключ к привлекательности и образец универсальной гармонии, которая завлекает человеческий глаз. Например, пластические хирурги часто упоминают о золотом сечении. Эта концепция также имеет большое значение для М. Ливио. Золотое сечение: история PHI, самого удивительного числа в математике, не имеющего аналогов среди других чисел.
Оно встречается в природе
Числа Фибоначчи и спирали, которые относятся к золотому сечению, нередко наблюдаются в природе. К примеру, они могут быть замечены в количестве лепестков на цветках или в формах различных растений.
Часть эолового растения. Фото.
Его можно найти в архитектуре и искусстве
«Божественные пропорции» можно обнаружить, например, на Парфеноне и в египетских пирамидах. Также существует распространенное мнение о том, что Мона Лиза была создана согласно числу f.
Почему универсальность золотого сечения является мифом
Однако при более внимательном анализе становится очевидным, что эта аналогия не так всеобъемлюща, как кажется.
Преувеличение божественности золотого сечения
Золотое сечение воспринимается как более важное, чем это есть на самом деле. Привлекательные узоры и элемент таинственности превратили его из простой геометрической аналогии в математический миф, ставший популярен среди, к примеру, нумерологов.
В большинстве случаев вопрос сводится к поиску компромисса, что подразумевает наличие значительных допущений. В таких ситуациях можно говорить о том, что точность и математическая универсальность отсутствуют. Поэтому, если вам угодно, вы сможете заметить «божественные концепции» повсюду вокруг.
Золотое сечение в природе встречается не так часто
Это далеко не обязательный принцип или правило, которое наблюдается повсеместно. К примеру, у цветка мака всегда имеется четыре лепестка, однако число Фибоначчи не включает значение четыре. Четырехлистные клеверы тоже нередки. Раковины морских моллюсков могут напоминать спирали золотого сечения, но все же они отличаются по структуре, как отметил Дж. Шарп. Спирали и золотое сечение / Сетевой журнал Nexus. У них больше оборотов спиралей, а расстояния между ними короче. Ни у одного из моллюсков коэффициент закрутки раковины не приближается к 1,62. Это можно заметить даже без специальных инструментов:

Спираль мидии. Иллюстрация.
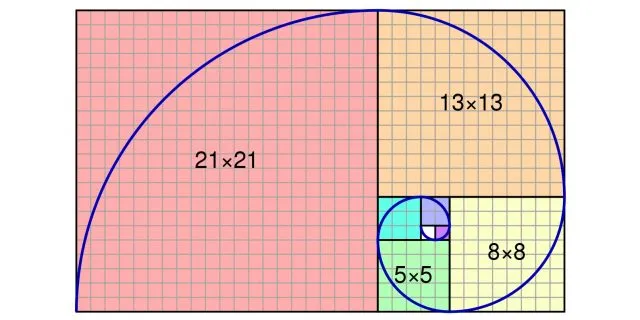
Спираль Фибоначчи вблизи золотого сечения. Изображение.
Человеческое тело изобилует множеством точек для измерений, что позволяет с легкостью находить проявления золотого сечения повсюду. Тем не менее, следует помнить, что «божественная пропорция» может располагаться в различных местах у разных людей, поскольку мы все уникальны.
В искусстве оно встречается довольно редко
Изучение 565 произведений известных мастеров живописи показало, что среднее соотношение сторон этих картин составляет 1,34 (A. Olariu, Золотое сечение и искусство живописи / arXiv Preprints). В данном случае явно отсутствует золотое сечение. Ученые, такие как М. Ливио в своей работе «Золотое сечение и эстетика» / Журнал «Плюс», отмечают, что даже в трудах Леонардо да Винчи его присутствие не всегда очевидно.
Археологические исследования не подтверждают существование P. Futakis. Древние греки строили с учетом принципа золотого сечения; в Кембриджском археологическом журнале также отмечается, что это соотношение могло быть применено при сооружении Парфенона. Из более чем 100 архитектурных памятников античной Греции лишь четыре объекта демонстрируют такое соответствие: башня, алтарь, гробница и надгробие. Даже у древних египтян, которые не обладали достаточными технологиями для точного вычисления пропорций, было сложно использовать золотое сечение.
Кому на самом деле полезно золотое сечение
Современная математика применяет концепцию золотого сечения, о чем рассказывает С. К. Карлсон. Золотое сечение и числа Фибоначчи играют важную роль в описании фракталов — фигур, показывающих самоподобие.
Фрактальная форма капусты Романеско. Фото.
Понимание f-числа имеет ключевое значение для анализа хаоса и динамических систем. Это знание помогает глубже осознать процессы, происходящие в природе, а также механизм самоорганизации.
Кроме того, последовательность Фибоначчи оказывается полезной при решении ряда сложных задач. Например, советский ученый Юрий Матиясевич применил эти числа в своем доказательстве относительно работы Ф.П. Варпаховского и А.Н. Колмогорова. Он затрагивал десятую проблему Гильберта/квантовую проблему, связанную с отсутствием универсального алгоритма для решения уравнений с двумя и более переменными.